Vettori: somma e prodotto scalare

Cosa sono i vettori? Quali operazioni si possono fare con i vettori?

Scopriamolo assieme nelle prossime pagine!

Un vettore è un elemento geometrico rappresentato da un segmento orientato (freccia) e caratterizzato da quattro elementi: 

• modulo: rappresenta la lunghezza del vettore (indicata da un valore e un’unità di misura);
• direzione: è individuata dalla retta su cui giace il vettore;
• verso: il verso è descritto dalla punta del vettore stesso, rappresentato da un segmento orientato

Capito questo vediamo che operazioni si possono fare con i vettori.

SOMMA

Consideriamo due vettori v e w.

La loro somma è un vettore che ha per componenti la somma delle componenti dei due vettori iniziali.

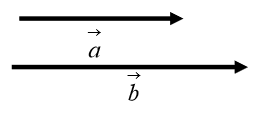
• Caso più semplice: vettori che hanno stessa direzione e stesso verso

La somma dei due vettori, sarà un vettore che avrà stessa direzione e stesso verso di entrambi e come modulo la somma dei moduli.

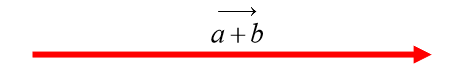
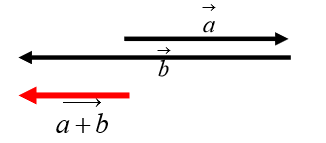
• Vettori discordi: vettori che hanno stessa direzione ma verso opposto.

La somma dei due vettori, sarà un vettore, che avrà stessa direzione, verso del vettore con modulo maggiore e come modulo la differenza tra i moduli

• Caso piú diffuso: vettori che formano un angolo α tra di loro

In termini geometrici corrisponde alla regola del parallelogramma. Il vettore somma giace sulla diagonale dell’ipotetico parallelogramma.

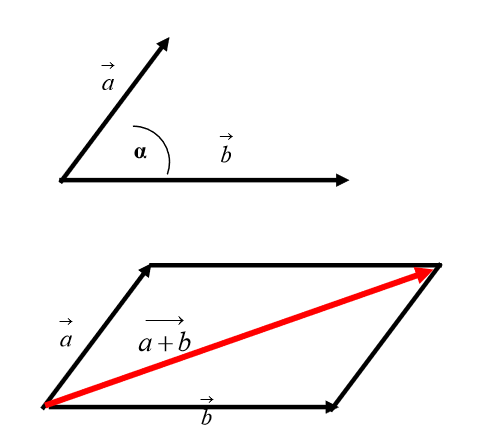
Se in un problema ci capiterá di dover sommare due vettori che non hanno lo stesso verso e la stessa direzione, il vettore somma non è dato dalla somma dei due moduli!!!!

Per sommare i due vettori prima di tutti si scompongono i vettori nelle loro componenti con le regole della trigonometria e solo dopo si sommano tra di loro le componenti in x e in y.

Per trovare il modulo del vettore risultante si applica il teorema di pitagora.

MOLTIPLICAZIONE PER UNO SCALARE

Dati il vettore v e il numero reale k il vettore kv ha come componenti quelle di v moltiplicate per k

Il nuovo vettore ha

• modulo dato dalle vecchie componenti di v moltiplicate per il modulo di k
• la direzione è quella di prima,non cambia
• il verso resta uguale se k è positivo e si inverte se k è negativo.

PRODOTTO SCALARE

È un operazione che, dati due vettori, ci dà un numero reale.

Dati due vettori v e u il loro prodotto scalare é dato dalla formula

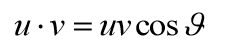
Si moltiplicano i moduli dei due vettori per il coseno dell’angolo compreso.

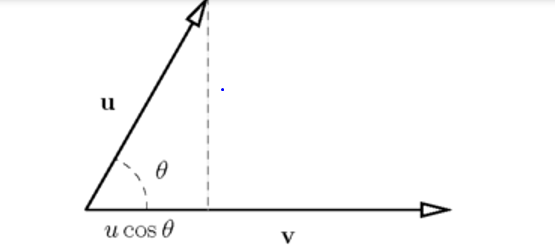
Dato che i due moduli rappresentano le lunghezze dei vettori che sono sempre quantità positive, Il segno del prodotto scalare è deciso dal coseno Dell angolo

Il prodotto scalare è nullo se almeno uno dei due vettori è il vettore nullo, oppure se essi sono tra loro perpendicolari

Queste erano le operazioni con i vettori  😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!