Uno e uno solo: un esercizio sugli zeri di una funzione

Bentornati per un altro esercizio di matematica! Oggi ci occupiamo di esistenza e unicità degli zeri di una funzione. Vedremo come alcuni risultati del programma di quinta superiore possano convogliare in un unico interessante esercizio. Buona lettura!

Esercizio. Sia data la funzione

\(f(x)=e^{3x} + x^3 + \arctan{7x}.\)

Dimostrare che \(f\) ammette uno e un solo zero in \(\mathbb{R}\).

Notiamo come il problema ci richieda di provare sia l’esistenza che l’unicità di tale zero, ossia di un punto \(x \in \mathbb{R}\) che soddisfi \(f(x)=0\). Inoltre, risulta evidentemente improbabile riuscire a risolvere tale equazione con i metodi classici a nostra disposizione. Insomma, dovremmo ingegnarci un po’.

Soluzione. Prima di tutto, tentiamo di capire l’andamento della funzione \(f\). Chiaramente essa risulta definita su tutto l’asse reale, e ivi continua e derivabile, essendo ottenuta componendo e sommando funzioni continue e derivabili. Non potendone studiare il segno, un’informazione utile potrebbe essere quella dei limiti agli estremi del dominio. Vale che
\(\lim_{x \to + \infty} f(x) = + \infty,\)
\(\lim_{x \to – \infty} f(x) = – \infty.\)
Un’ultima caratteristica della funzione può essere dedotta dallo studio della derivata:
\(f'(x)=3e^{3x} + 3x^2 + \frac{7}{1+49x^2}.\)
\(f'(x)\) risulta essere la somma di tre quantità: la prima e l’ultima sempre strettamente positive, la seconda positiva o nulla. Di conseguenza,
\(f'(x)>0 \ \forall x \in \mathbb{R}.\)
Utilizzando un corollario del teorema di Lagrange, deduciamo che \(f\) è una funzione strettamente monotona crescente su \(\mathbb{R}\). Il grafico della funzione \(f\) risulterà qualcosa di questo tipo:

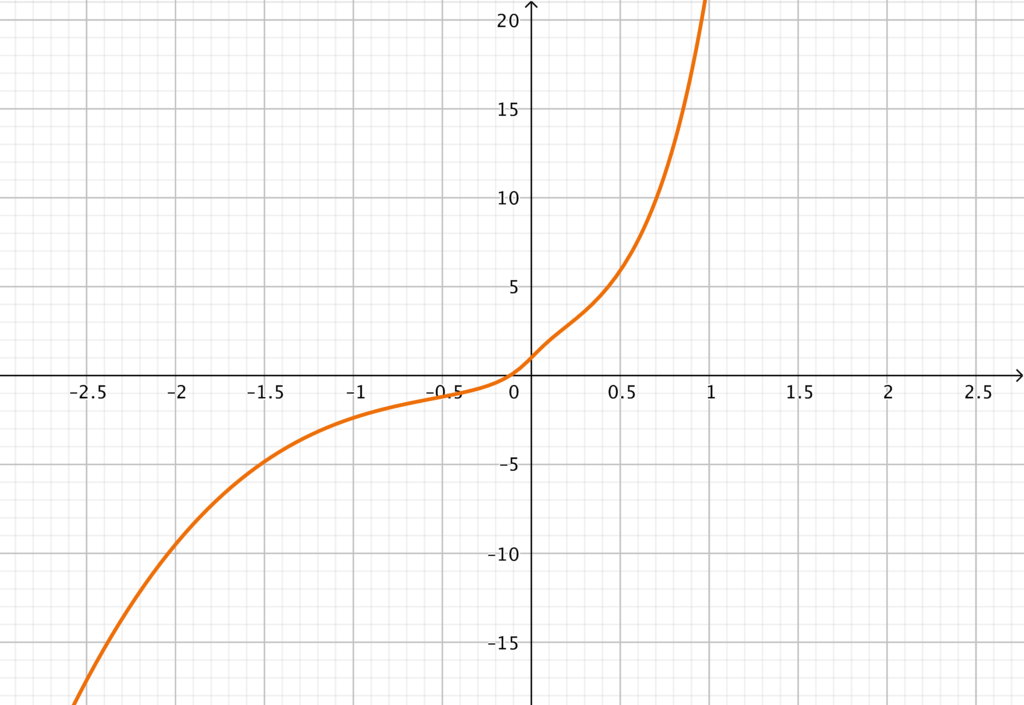
Dall’immagine riportata effettivamente la funzione \(f\) sembra ammettere uno e un solo zero. Come possiamo giustificare questo fatto, senza essere in grado di trovare esplicitamente la soluzione?

Una prima osservazione è che, da quanto già dedotto sull’andamento della funzione, se uno zero esiste allora questo è necessariamente unico! Infatti, la funzione \(f\) è strettamente crescente, avendo derivata positiva su tutto l’asse reale.

Dobbiamo quindi confrontarci con l’esistenza di tale zero. L’idea è quella di utilizzare, guarda a caso, un teorema che sembra esser fatto apposta per noi: il teorema di esistenza degli zeri. Questo afferma che

Teorema. (Esistenza degli zeri) Sia \(f\) una funzione da un intervallo chiuso limitato \([a,b]\) in \(\mathbb{R}\), continua in \([a,b]\), tale che \(f(a)\) e \(f(b)\) siano discordi. Allora esiste almeno un \(c \in (a,b)\) tale che \(f(c)=0\).

Si tratta ora di fare un poco di attenzione al dominio di definizione: abbiamo bisogno di un opportuno intervallo chiuso e limitato dove poter applicare il teorema. In particolare, essendo la funzione già continua sull’intero \(\mathbb{R}\), cerchiamo un intervallo \([a,b]\) in cui \(f(a)<0\) e \(f(b)>0\) (non potrebbe accadere il contrario, essendo la funzione crescente). La sfida è quella di non utilizzare la calcolatrice! Potremmo provare a inserire qualche valore per \(x\) per determinare \([a,b]\). Ad esempio,
\(f(0)=1>0\).
Poniamo dunque \(b=0\).
Calcoliamo invece
\(f(-1)=e^{-3} -1 + \arctan{-7}.\)
Sappiamo che \(\arctan{-7}<0\), e che \(e^{-3}<1\), e dunque \(e^{-3}-1<0\). In conclusione,
\(f(-1)<0\).
Poniamo \(a=-1\). Abbiamo trovato un possibile intervallo che soddisfa le ipotesi richieste! Abbiamo quindi mostrato che tale zero esiste; avendone già mostrato l’unicità, abbiamo finito l’esercizio. Inoltre, siamo stati in grado di localizzare lo zero tra \(-1\) e \(0\). Una possibile richiesta successiva potrebbe essere applicare il metodo di bisezione per approssimare lo zero della funzione.

Un ultima nota: si potrebbero addirittura evitare le stime fatte sulla valutazione della funzione \(f\) in qualche punto utilizzando la definizione di limite. Saresti in grado di farlo? Provaci!

Questo era un esercizio sugli zeri di una funzione 😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!