Un esercizio sul teorema della media integrale

In questo articolo risolveremo un esercizio sul teorema della media integrale, che può essere esemplicativo dell’utilizzo di questo teorema e giustifica, in qualche modo, il suo nome.

Cominciamo con il ricordare il teorema della media integrale.

Teorema della media. Sia \(f:[a,b]\to \mathbb{R}\) una funzione continua sull’intervallo \([a,b]\). Allora esiste un punto \(x_0\in [a,b]\) tale che

\(\frac{1}{b-a}\int_a^bf(t)dt=f(x_0)\).

La quantità \(\frac{1}{b-a}\int_a^b f(t)dt\) si chiama media integrale della funzione \(f\) sull’intervallo \([a,b]\).

Il teorema ha anche un’interpretazione geometrica non banale. Disegnamo infatti il grafico della funzione \(f\) su \([a,b]\). Ricordiamo ora che \(\int_a^bf(t)dt\) rappresenta la misura dell’area sottesa dal grafico della funzione tra \(a\) e \(b\), e osserviamo che l’uguaglianza del teorema può essere riscritta come \((b-a)f(x_0)=\int_a^b f(t)dt\).

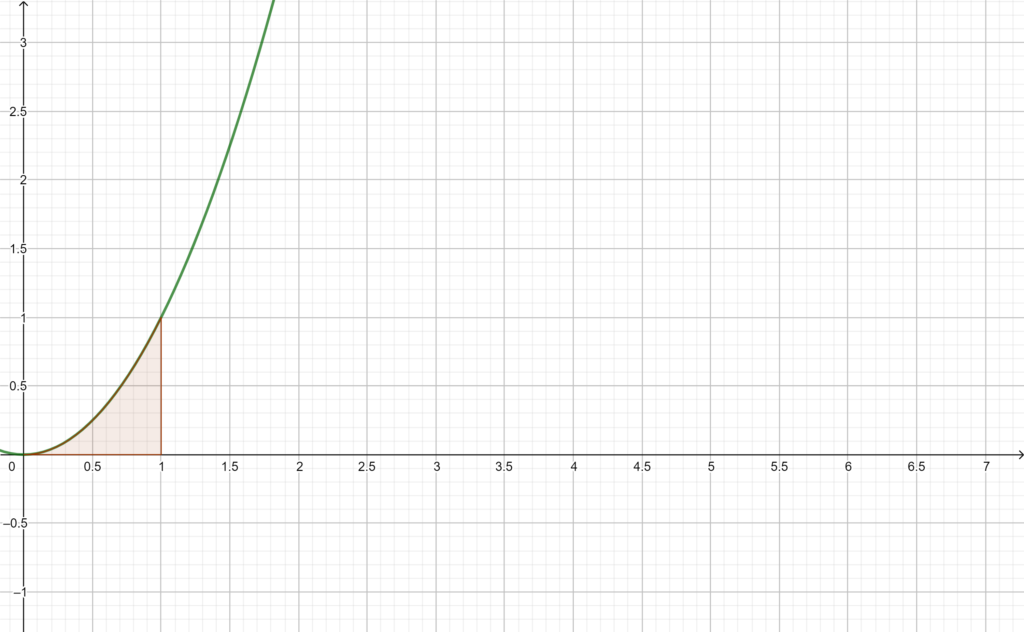
\((b-a)f(x_0)\) rappresenta invece l’area di un rettangolo avente base \([a,b]\) e altezza \(f(x_0)\). Pertanto il teorema afferma che esiste un \(x_0\in [a,b]\) che permette di calcolare l’area sottesa dal grafico della funzione con l’area di un rettangolo, avente base \([a,b]\) e altezza \(f(x_0)\).

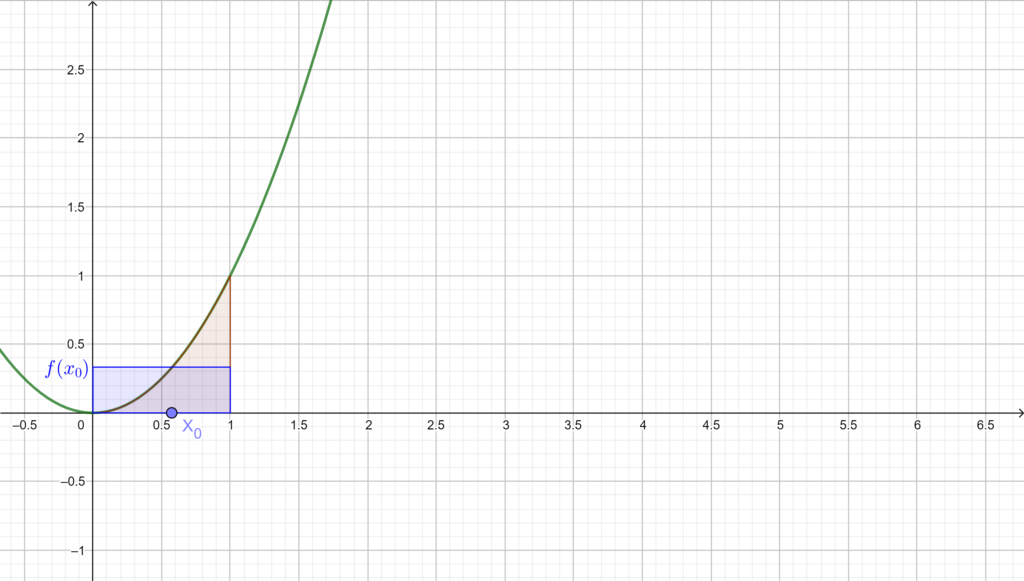
Come promesso, passiamo ora alla risoluzione di un esercizio sul teorema della media.

Esercizio. In un tratto autostradale, nel tempo \([t_1,t_2]\), la velocità di un’automobile segue la legge \(v(t)\).

1) Quanto è lungo il tratto stradale considerato?

2) Qual è la velocità media della macchina?

3)Se \(t_1=0 h\). \(t_2=0.5 h\), \(v(t)=100+20\pi cos(\pi t)\) e \(L=130 km/h\) è il limite di velocità, dimostrare (usando il teorema della media) che c’è stato un istante \(t^*\in [t_1,t_2]\) in cui la macchina era sopra al limite di velocità.

4)Scrivere la funzione posizione \(x(t)\) dell’automobile, in un sistema di riferimento rispetto al quale al tempo \(t=0\) l’automobile aveva una distanza \(x_0=10 km\) dall’origine.

Soluzione dell’esercizio.

1)Un’idea per calcolare la distanza percorsa potrebbe essere la seguente: sia \(x(t)\) una primitiva della funzione velocità \(v(t)\): è chiaro che questa misura la distanza da un certo punto fissato al tempo \(t\), dunque per calcolare la lunghezza del tratto autostradale è sufficiente valutare la differenza \(x(t_2)-x(t_1)\). La formula fondamentale del calcolo integrale ci viene in soccorso, dicendoci che, se \(x(t)\) è una primitiva di \(v(t)\) su \([t_1,t_2]\), allora \(x(t_2)-x(t_1)=\int_a^b v(t)dt\). Quindi questa è la lunghezza del tratto autostradale.

2) Ricordiamo che \(v_m=\frac{\Delta x}{\Delta t}\). Nel nostro caso \(\Delta x\) è la lunghezza del tratto autostradale, appena calcolata, mentre \(\Delta t\) è \(t_2-t_1\). Perciò la velocità media è \(v_m=\frac{1}{t_2-t_1}\int_{t_1}{t_2}v(t)dt\): è interessante notare come la media integrale della funzione velocità tra \(t_1\) e \(t_2\) sia proprio la velocità media dell’automobile tra \(t_1\) e \(t_2\).

3) Cerchiamo di utilizzare il teorema della media: siccome la funzione \(v(t)=100+20\pi\cos{\pi t}\) è continua, allora esiste \(t^*\in[t_1,t_2]=[0,0.5]\) tale per cui \(v(t^*)=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}v(t)dt=v_m\). Dunque, per dimostrare l’esistenza di un istante in cui la velocità istantanea dell’automobile ha superato il limite, è sufficiente dimostrare che \(v_m>L\). Calcoliamo allora $v_m$, partendo dalla valutazione dell’integrale definito. \(\int_0^{0.5}100+20\pi\cos{\pi t} dt= 100t+20\sin{\pi t}+c|_{t=0}^{t=0.5}\)

\(=50+20\cdot 1 – (0)=70\). Dunque la lunghezza del tratto autostradale è di \(70 km\). Pertanto \(v_m=\frac{70}{0.5}=140 km/h>130 km/h=L\). La velocità media è superiore al limite e, in base a quanto abbiamo già detto, questo basta a concludere.

4) Per scrivere la legge di posizione è sufficiente calcolare una primitiva della funzione \(v(t)\): questo calcolo è già stato fatto al punto precedente e possiamo affermare che la famiglia di primitive della funzione velocità assegnata nell’intervallo \([0,0.5]\) sono le \(x(t)=100t+20\sin{\pi t}+c\), al variare di \(c\in\mathbb{R}\). Per trovare la funzione posizione desiderata, dobbiamo leggere le richieste del problema. Al tempo \(t=0\) la distanza dall’origine è \(x(0)=10 km\), quindi \(x(0)=100\cdot 0+20\sin{0}+c=10\), pertanto \(c=10\) e \(x(t)=10+100t+20\sin{\pi t}\) è la funzione posizione richiesta.

Questo era un esercizio sul teorema della media  😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!