Tra due tangenti: un esercizio sulle derivate

Oggi proponiamo un esercizio sulle derivate che racchiude alcune idee importanti, che spesso e volentieri possono essere utilizzate per la risoluzione di altri quesiti. Saprai risolvere il problema prima di leggerne la soluzione?

Problema. Il testo proposto è qui riportato:

Consideriamo le due funzioni
\(f_1(x)=e^x +x\),
\(f_2(x)=\textrm{arctg}(x)-2(x+1)^3+3\).
Determinare tutti i punti di intersezione dei grafici delle due funzioni. In tali punti, determinare l’ampiezza dell’angolo formato dai due grafici.

Apparentemente le espressioni delle due funzioni potrebbero scoraggiarci, ma vedremo che un paio di trucchetti ci permetteranno di concludere l’esercizio.

Soluzione. Iniziamo l’esercizio studiando i punti di intersezione dei grafici. Un generico punto del grafico di \(f_1(x)\) è della forma \((x, f_1(x))\); similmente, un punto del grafico di \(f_2(x)\) è del tipo \((x, f_2(x))\). Poiché siamo alla ricerca dei punti comuni ai due grafici, possiamo equivalentemente determinare per quali \(x \in \mathbb{R}\) vale
\(f_1(x)=f_2(x) \Rightarrow f_1(x)-f_2(x)=0\).
Questo ci porta allo studio degli zeri della funzione \(f_1(x)-f_2(x)\) mediante l’equazione
\(e^x + x – \textrm{arctg}(x) + 2(x+1)^3 +3=0\),
che apparentemente risulta impossibile da risolvere. Ecco qui il primo trucchetto: deriviamo la funzione \(f_1(x)-f_2(x)\), ottenendo
\(e^x + 1 – \frac{1}{1+x^2} +6(x+1)^2 =\)
\(e^x + \frac{x^2}{1+x^2} + 6(x+1)^2\).
Notiamo che per ogni \(x \in \mathbb{R}\) vale che
\(e^x>0, \ \frac{x^2}{1+x^2}\ge 0, \ 6(x+1)^2\ge 0\);
raggruppando il tutto ricaviamo
\(e^x + \frac{x^2}{1+x^2} + 6(x+1)^2 >0\),
ossia \((f_1-f_2)'(x)>0\) per ogni \(x \in \mathbb{R}\). Per un corollario del Teorema di Lagrange, questo implica che la funzione \(f_1(x)-f_2(x)\) è strettamente crescente! Dunque, se esiste un \(a \in \mathbb{R}\) tale per cui \(f_1(a)-f_2(a)=0\), tale \(a\) è necessariamente unico! Se ci fossero infatti due punti diversi \(a, b \in \mathbb{R}\), con \(a<b\), tali per cui \(f_1(a)-f_2(a)=0\) e \(f_1(b)-f_2(b)=0\), la funzione \(f_1(x)-f_2(x)\) non sarebbe strettamente crescente.

Bene, abbiamo ottenuto una prima informazione. L’equazione, però, resta comunque molto difficile a vista. Non è mica che l’esercizio è costruito apposta per poter determinare a mano una soluzione, e argomentare come fatto sopra per dire che questa soluzione è unica? (Sì, è fatto apposta, ma capita davvero spesso.) Insomma, perché non provare? Guardiamo l’equazione
\(e^x + x = \textrm{arctg}(x) -2(x+1)^3 + 3\).
Proviamo a inserire qualche valore, tra quelli più semplici, per farci un’idea. Basta poco per notare che \(a=0\) è soluzione. Infatti, \(f_1(0)=1\) come pure \(f_2(0)=1\). In conclusione, l’unico punto di intersezione tra i grafici è dato da \((0,1)\). Qui sotto un’immagine chiarirà le idee.

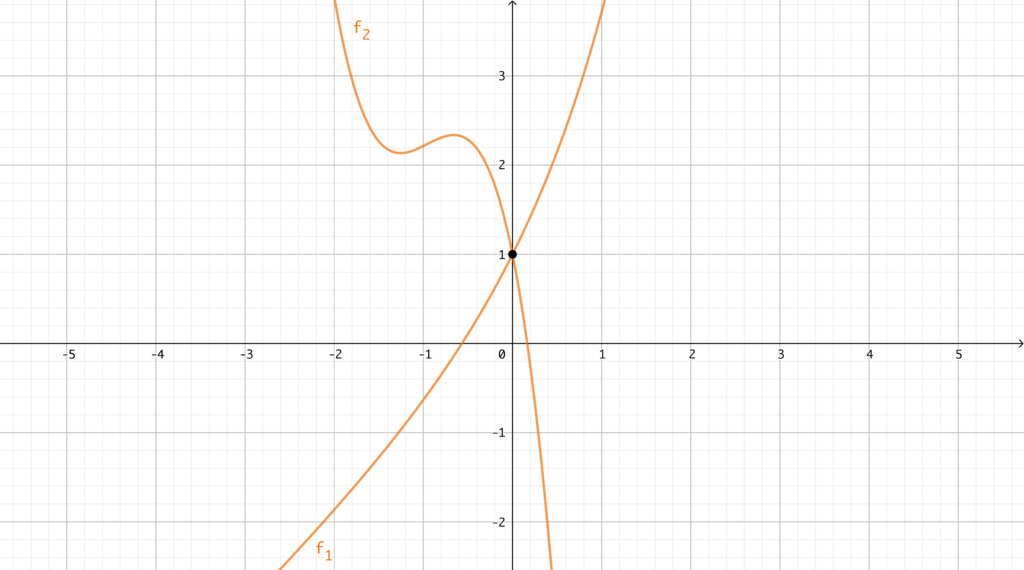
Veniamo dunque alla seconda parte dell’esercizio. Che cos’è l’angolo formato dai due grafici nel punto di intersezione? Per definizione, non è nient’altro che l’angolo determinato dalle rette tangenti ai grafici delle funzioni in tale punto. Di nuovo, l’intuizione ci porta a usare le derivate. Infatti, la derivata di una funzione valutata in un’ascissa è il valore del coefficiente angolare della retta tangente al grafico della funzione nel punto di tale ascissa. Inoltre, c’è un legame tra il coefficiente angolare \(m\) di una retta e l’angolo \(\alpha\). formato con l’asse delle \(x\):
\(m=\textrm{tg} (\alpha)\). Calcoliamo quindi i due coefficienti angolari.
\((f_1)'(x)=e^x+1 \Rightarrow\)
\(m_1=(f_1)'(0)=2\);
\((f_2)'(x)=\frac{1}{1+x^2} -6(x+1)^2 \Rightarrow\)
\(m_2=(f_2)'(0)=-5\).
Se ora chiamiamo \(m_1=\textrm{tg}(\alpha_1), \ m_2=\textrm{tg}(\alpha_2)\), siamo interessati alla differenza \(\alpha_1 – \alpha_2\), l’angolo compreso tra le due rette.

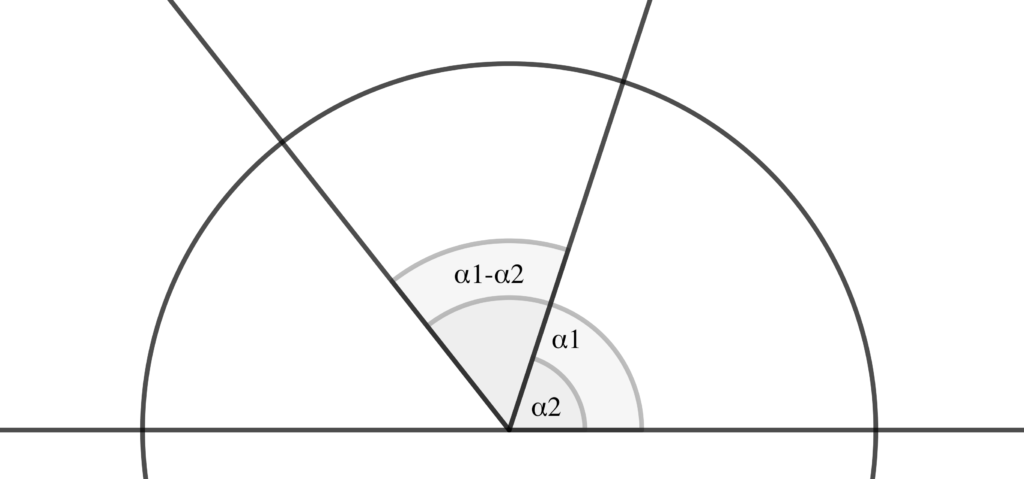
Vogliamo trovare \(\alpha_1 – \alpha_2\) conoscendo le tangenti degli angoli in questione… qui c’è puzza di formule trigonometriche della tangente di somma e differenza. Per una volta ci tocca; tuttavia, non sono così complicate! È inutile ricordarsele a memoria, si possono ricavare usando le formule di seno e coseno! Infatti:
\(\textrm{tg}(\alpha_1 – \alpha_2)=\frac{\sin (\alpha_1 – \alpha_2)}{\cos (\alpha_1 – \alpha_2)} =\)
\(=\frac{\sin(\alpha_1)\cos(\alpha_2)-\cos(\alpha_1)\sin(\alpha_2)}{\cos(\alpha_1)\cos(\alpha_2) + \sin(\alpha_1)\sin(\alpha_2)}\);
dividendo numeratore e denominatore per \(\cos(\alpha_1)\cos(\alpha_2)\) (operazione che lascia invariato il rapporto) otteniamo
\(\frac{\textrm{tg}(\alpha_1)-\textrm{tg}(\alpha_2)}{1+\textrm{tg}(\alpha_1)\textrm{tg}(\alpha_2)}\).
Ecco fatto, nulla di trascendente. Da questo otteniamo
\(\textrm{tg}(\alpha_1-\alpha_2)=\frac{m_1-m_2}{1+m_1m_2}=\)
\(\frac{2+5}{1-2\cdot 5}=-7/9\).

Ora bisogna fare un po’ di attenzione, per evitare di cadere in un paio di tranelli. Prima di tutto, potrebbe sembrare dal grafico che avremmo dovuto considerare la somma degli angoli \(\alpha_1\) e \(\alpha_2\), e non la differenza. Non facciamoci ingannare! Uno dei due angoli è negativo (in quanto il grafico di \(f_2(x)\) ha pendenza negativa in \((0,1)\)) e dunque la differenza, in questo caso, ha ampiezza maggiore di quella degli angoli considerati; è lei l’operazione giusta. Inoltre, facciamo attenzione a un errore più grave: non vale che \(\alpha_1 – \alpha_2 = \textrm{arctg}(-7/9)\). Infatti, se così fosse, \(\alpha_1 – \alpha_2\) dovrebbe essere un angolo negativo (ossia orientato in senso orario) di ampiezza minore di \(\pi/2\). Tuttavia il grafico ci suggerisce che questo non sia affatto vero!

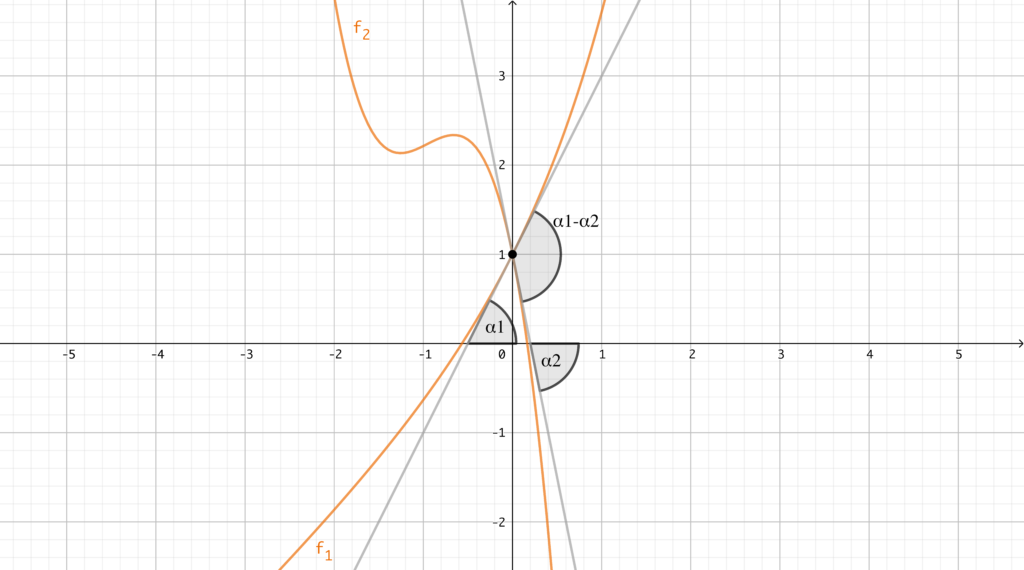
Come mai tutto questo accade? Questo spiacevole inconveniente è dovuto al fatto che la funzione \(\textrm{tg}\) non è invertibile, a meno che non venga ristretta all’intervallo \((0,\pi/2)\), e solo qui la sua inversa è la funzione \(\textrm{arctg}\). Dunque \(\alpha_1 – \alpha_2\) non è \(\textrm{arctg}(-7/9)\), ma è uno dei possibili angoli che ha per tangente \(-7/9\), ossia vale
\(\alpha_1 – \alpha_2 = \textrm{arctg}(-7/9) + k\pi\),
per un opportuno \(k \in \mathbb{Z}\). Poiché \(\alpha_1 – \alpha_2\) risulta dal grafico essere compreso tra \(0\) e \(\pi\), si ha \(k=1\) e
\(\alpha_1 – \alpha_2 = \pi + \textrm{arctg}(-7/9)=\)
\(=\pi – \textrm{arctg}(7/9)\),
in quanto \(\textrm{arctg}\) è dispari. Questo conclude l’esercizio.

Se qualcuno di voi, provando a risolvere l’esercizio, avesse trovato come soluzione alla seconda parte il numero
\(\textrm{arctg}(2)+\textrm{arctg}(5)\),
non si preoccupi: anche questo risultato è giusto, anzi, si ottiene ancor più velocemente. Si può ricavare semplicemente eseguendo la differenza degli angoli \(\alpha_1\) e \(\alpha_2\) determinati applicando \(\textrm{arctg}\) ai coefficienti angolari \(m_1\) e \(m_2\). Ho però preferito proporvi questa soluzione per mostrarvi i possibili sgambetti che il problema ci può tirare. Inoltre, poiché entrambe le soluzioni sono corrette, esse sono uguali!
\(\textrm{arctg}(2)+\textrm{arctg}(5)=\pi-\textrm{arctg}(7/9)\).
In particolare, abbiamo involontariamente dimostrato che vale l’uguaglianza
\(\textrm{arctg}(2)+\textrm{arctg}(5)+\textrm{arctg}(7/9)=\pi\).

Questo era un esercizio tra due tangenti 😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!