Integrale definito

Siete in grado di calcolare l’area sottesa da una curva in un piano cartesiano? Oggi cercheremo di rispondere a questa domanda nel caso in cui la curva sia il grafico di una funzione con particolari proprietà. Il nostro approccio sarà simile a quello utilizzato dal matematico Bernhard Riemann.

Mettiamo bene in luce il nostro obiettivo: data una funzione limitata \(f:[a,b]\to \mathbb{R}\), vogliamo calcolare l’area sottesa dal grafico di \(f\), rappresentata in figura.

Una prima intuizione può essere quella di approssimare quest’area con aree elementari che siamo in grado di calcolare, ad esempio le aree dei rettangoli.

Fissiamo dunque \(n\in\mathbb{N}\). Dividiamo \([a,b]\) in \(n\) intervalli di ampiezza \(\frac{b-a}{n}\) e chiamiamo \(I_k\) il \(k\)-esimo intervallo. Per ogni \(k=0,\dots,n\) definiamo

\(l_k := sup_{x\in I_k}f(x) \quad L_k := inf_{x\in I_k}f(x). \)

Osserviamo che \(l_k\) e \(L_k\) sono finiti perchè abbiamo supposto \(f\) limitata. A questo punto abbiamo due approssimazioni dell’area che vogliamo calcolare, una dall’alto e una dal basso. Definiamo quindi

\( S_n(f):= \sum_{k=1}^n L_k \frac{b-a}{n} \quad s_n(f):=\sum_{k=1}^n l_k \frac{b-a}{n}. \)

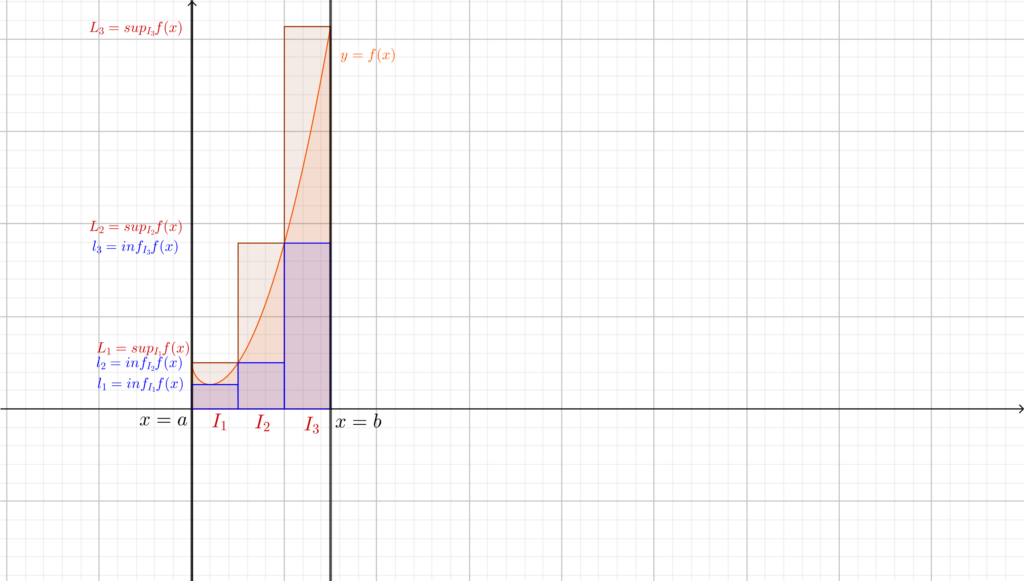
Il significato di queste due scritture è il seguente: \(S_n(f)\) rappresenta la somma delle aree dei rettangoli (di base \(\frac{b-a}{n} \) e altezza \(L_k\)) che approssimano dall’alto la funzione; analogamente \(s_n(f)\) rappresenta la somma delle aree dei rettangoli che la approssimano dal basso. Fungono pertanto come una \(n\)-esima approssimazione dell’area che vogliamo calcolare. \(S_n(f)\) prende anche il nome di somma superiore n-esima, e analogamente \(s_n(f)\) sarà la somma inferiore n-esima. In effetti le definizioni “superiore” e “inferiore” sono sensate, in quanto non è difficile rendersi conto che \(\forall n\in\mathbb{N}\) \(s_n(f)\le Area(f) \le S_n(f)\).

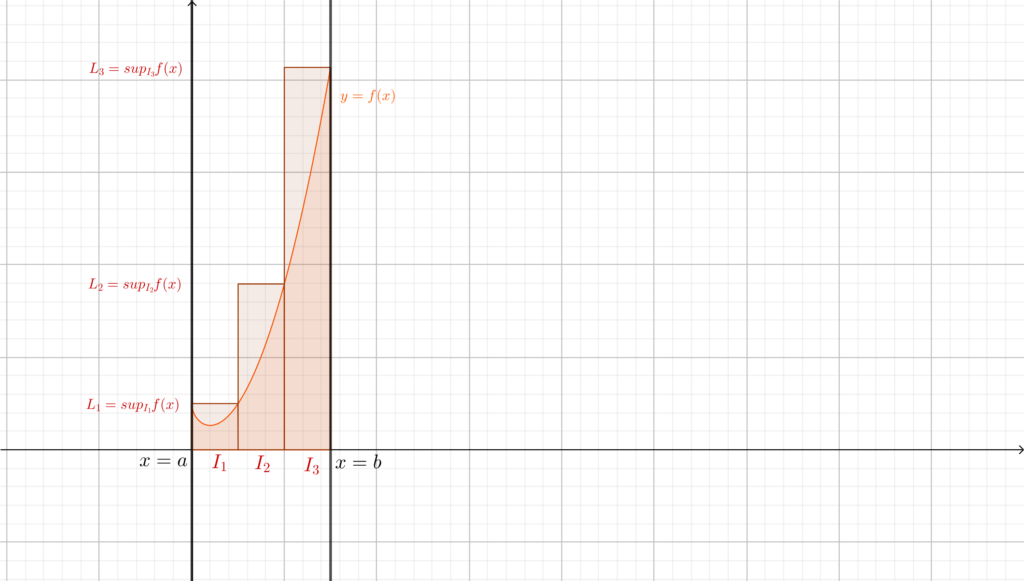
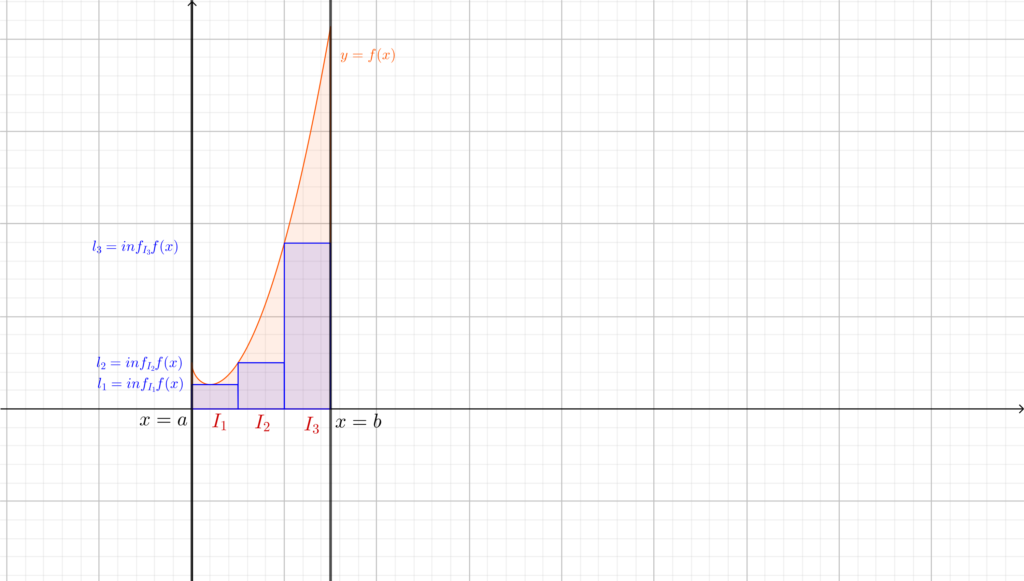
Qual è l’idea per ottenere l’area sottesa dal grafico di \(f\)? Passare al limite.

Data \(f:[a,b]\to \mathbb{R}\) limitata, diciamo che \(f\) è R-integrabile (o integrabile secondo Riemann o, più brevemente, integrabile) sull’intervallo \([a,b]\) se \(lim_{n\to +\infty}s_n(f)=lim_{n\to +\infty} S_n(f)\). In tal caso chiamiamo \(\int_a^b f(x)dx\) il valore di tale limite, che prende il nome di integrale definito di \(f\) nell’intervallo \([a,b]\).

Qual è il significato dell’integrale definito? Può essere pensato come una somma di infiniti termini infinitesimi. Infatti, intendendo \(\int_a^b f(x)dx\) come il limite della somma di rettangoli, otteniamo che il numero di intervalli è diventato infinito, dunque è infinito il numero di termini nella sommatoria, mentre i termini sommati risultano essere infinitesimi (i.e. tendenti a zero), in quanto \(dx\) rappresenta l’ampiezza dell’intervallo \(\frac{b-a}{n}\) diventata una quantità tendente a zero, raffigurante un piccolo spostamento sull’asse delle ascisse. Per quanto riguarda l’altezza dei rettangoli, essendo questi di base molto piccola (\(dx\)), può essere assimilabile al valore di \(f\) in \(x\), mentre \(x\) varia nell’intervallo \([a,b]\).

Il fatto che abbiamo imposto nella definizione di Riemann-integrabilità che i due limiti siano uguali lascia pensare che questo non accada sempre, dunque sorge una domanda: se \(f\) è limitata su \([a,b]\), è sempre vero che \(lim_{n\to +\infty}s_n(f)=lim_{n\to +\infty}S_n(f)\)? Chiaramente la risposta è no, e ora mostrerò un esempio di funzione in cui questa cosa non accade. La funzione che sto per introdurre si chiama funzione di Dirichlet.

Sia \(f:[0,1]\to \mathbb{R}\) definita “a tratti”.
\(f(x):=\)
\begin{cases}

• \(1\) se \(x\in[0,1]\cap \mathbb{Q}\);
• \(0\) altrimenti.

Sostanzialmente si tratta di una funzione che vale \(1\) se \(x\) è razionale, \(0\) se \(x\) è irrazionale. Chiaramente si tratta di una funzione limitata perchè assume solo i due valori \(0\) e \(1\).

Fissiamo \(n\in\mathbb{N}\) e cerchiamo di capire quanto valgono \(s_n(f)\) e \(S_n(f)\). Poichè in ogni intervallo reale è presente almeno un razionale e almeno un irrazionale, allora \(\forall k=0,\dots,n\) all’interno di \(I_k\) c’è almeno un \(x_{k0}\) tale per cui \(f(x_{k0})=0\) e almeno un \(x_{k1}\) tale per cui \(f(x_{k1})=1\). Pertanto \(l_k=0\) e \(L_k=1\) per ogni \(k=0,\dots,n\).\
Perciò, ricordando che nel nostro caso \([a,b]=[0,1]\), allora

\(s_n(f)=\sum_{k=1}^n l_k \frac{1-0}{n}=\)

\(=\sum_{k=1}^n 0 \cdot \frac{1}{n}=0 \quad \forall n\in \mathbb{N};\)

\(S_n(f)= \sum_{k=1}^n L_k \cdot \frac{1-0}{n}=\)

\(=\sum_{k=1}^n 1\cdot \frac{1}{n}=n\cdot \frac{1}{n}=1 \quad \forall n\in\mathbb{N}.\)
Dunque la somma inferiore \(n\)-esima è 0 e la somma superiore \(n\)-esima è 1 per ogni \(n\in\mathbb{N}\). Pertanto

\( lim_{n\to +\infty}s_n(f)=lim_{n\to +\infty}0=0\)

\(lim_{n\to +\infty}S_n(f)=lim_{n\to +\infty}1= 1.\)
Dunque i due limiti sono diversi: la funzione di Dirichlet è limitata ma non è R-integrabile su \([0,1]\).

Cerchiamo allora delle condizioni che garantiscano la R-integrabilità, e in particolare ne citiamo due, senza però dimostrarle.
In primo luogo, se \(f\) è continua su \([a,b]\), allora \(f\) è R-integrabile su \([a,b]\). \
Inoltre, se \(f\) è limitata su \([a,b]\) e ammette un numero finito di punti di discontinuità su \([a,b]\), allora \(f\) è R-integrabile. In effetti questa condizione è sensata, basti pensare alla seguente funzione, definita su \([0,2]\):

\(f(x)=\)

• \(1\) se \(x\in[0,1]\);
• \(2\) se \(x\in (1,2]\).

Nonostante questa funzione non sia continua, ha senso parlare di area sottesa dal grafico di questa funzione, ed è anche semplice calcolarla: è pertanto ragionevole assumere che questa funzione sia R-integrabile su \([0,2]\).

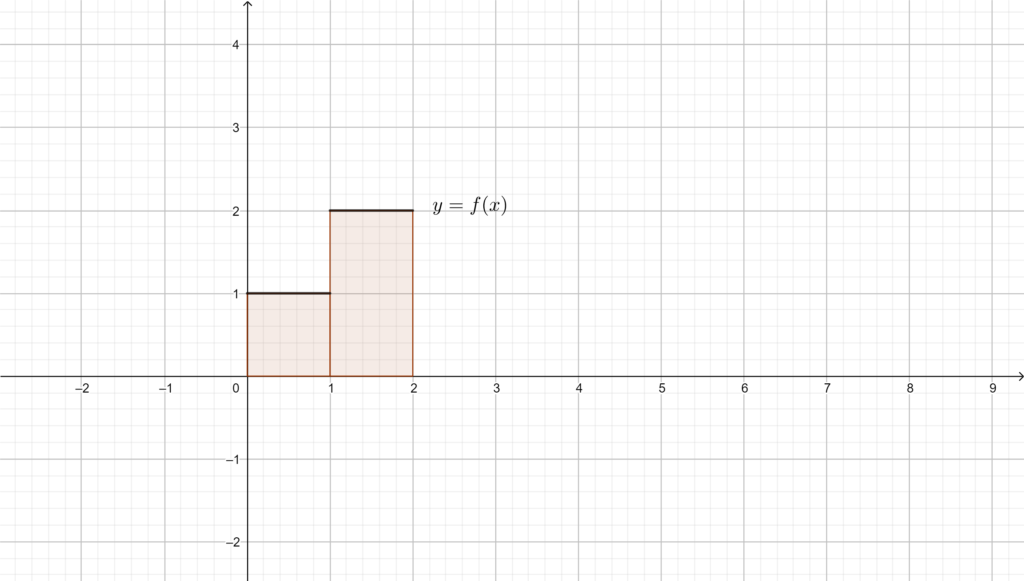
Entrambe le condizioni citate sono condizioni sufficienti per la R-integrabilità, ma è anche utile osservare che condizione necessaria è la limitatezza di \(f\) su \([a,b]\), condizione di cui non possiamo fare a meno, dato che è richiesta nella definizione. Nel secondo dei due casi citati, infatti, è stata esplicitamente richiesta. Nel primo caso, invece, in cui è stata richiesta la continuità, non abbiamo fatto alcuna richiesta di limitatezza: perchè? Il motivo è che il fatto che la funzione \(f\) sia continua sull’intervallo chiuso e limitato \([a,b]\) garantisce automaticamente la limitatezza, in quanto sono soddisfatte le ipotesi del teorema di Weierstrass.

Finora abbiamo osservato, dunque, che nel caso in cui una funzione sia R-integrabile su un intervallo chiuso e limitato \([a,b]\) è possibile calcolarne l’area sottesa dal grafico mediante il limite dell’approssimazione con rettangoli. In alcuni casi risulta semplice calcolare questo limite, mentre in altri casi tale calcolo è molto complicato, perciò è necessario uno strumento più potente per calcolare \(\int_a^b f(x)dx\).

Questo strumento è il teorema fondamentale del calcolo integrale, che, sotto opportune ipotesi, metterà in relazione la ricerca delle primitive di una funzione e il calcolo dell’area sottesa dal suo grafico.

Questo era l’integrale definito!  😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!