Lagrange vi spiega perchè prendete una multa

In autostrada spesso gli automobilisti si imbattono nei “Safety Tutor”. Sapete cosa sono? Vi hanno mai fatto prendere una multa? Dovete sapere che alla base della dimostrazione del superamento del limite di velocità c’è un noto teorema dell’analisi matematica: il teorema di Lagrange.

Prima di tutto, cerchiamo di capire cos’è un Safety Tutor. Si tratta di un sistema di controllo della velocità introdotto in alcuni tratti della rete autostradale italiana dal 2004. Questo consiste nella presenza di due centrali di rilevamento poste a diversi chilometri di distanza. Sostanzialmente si registra quanto tempo è trascorso tra il passaggio per la prima stazione di rilevamento e la seconda. A questo punto calcolare la velocità media è un gioco da ragazzi: \(v_m=\frac{\Delta x }{\Delta t}\), dove \(\Delta x\) è la distanza tra le stazioni e \(\Delta t\) è il tempo di percorrenza registrato dal Safety Tutor. Ora, se la velocità media è maggiore del limite di velocità, prenderemo una multa, altrimenti no! Beh, calma… La conclusione non è così scontata, soprattutto per dei pignoli come noi matematici.

D’altra parte quello che il Safety Tutor vuole mostrare è che nel nostro percorso c’è stato un istante in cui la nostra velocità istantanea è stata superiore al limite, altrimenti non avrebbe le “prove” per poterci dare una multa. Il Safety Tutor, tuttavia, è in grado di restituirci solo una velocità media. La domanda a cui vogliamo rispondere è dunque la seguente:

Il fatto che in un tratto di strada la velocità media della nostra automobile nell’intervallo di tempo \([t_1,t_2]\) fosse superiore al limite di velocità implica che c’è stato un istante tra \(t_1\) e \(t_2\) in cui la velocità istantanea fosse superiore al limite?

La risposta, che sembrerebbe scontata, è tutt’altro che banale. Per rispondere proviamo a matematizzare il problema.

Chiamiamo \(x(t)\) la funzione posizione che indica, al variare del tempo \(t\), la posizione (in metri) che la nostra automobile assume rispetto a un punto d’origine (supponiamo il casello autostradale). Chiamiamo poi \(x_1\) e \(x_2\) le posizioni delle due centrali di rilevazione del Safety Tutor (supponendo \(x_1<x_2\)) e analogamente \(t_1\) e \(t_2\) gli istanti di tempo tali per cui \(x(t_1)=x_1\) e \(x(t_2)=x_2\). Infine denotiamo con \(L\) il limite di velocità e \(v_m=\frac{x_2-x_1}{t_2-t_1}\) la velocità media registrata dal Safety Tutor, sapendo che \(v_m>L\).

Vogliamo ora definire la funzione velocità \(v(t)\), che esprime la velocità istantanea della nostra automobile nel corso del suo viaggio. Per definizione, la velocità istantanea rappresenta la velocità media dell’automobile in un intervallo di tempo infinitesimo, oppure, in termini differenziali, la derivata temporale della funzione posizione. Infatti

\(v(t_0)=\lim_{t\to t_0}\frac{x(t)-x(t_0)}{t-t_0}=x'(t_0)\).

Dunque la funzione velocità (istantanea) sarà \(v(t)=x'(t)\). Dopo questa rilettura , la nuova domanda a cui si vuole rispondere è la seguente:

Sapendo che \(v_m=\frac{x(t_2)-x(t_1)}{t_2-t_1}>L\) possiamo affermare che esiste \(t* \in [t_1,t_2]\) tale per cui \(v(t*)=x'(t*)>L\)?

Per rispondere alla nostra domanda viene in soccorso il teorema di Lagrange, che riportiamo di seguito.

Sia \(f:[a,b]\to \mathbb{R}\) una funzione continua nell’intervallo \([a,b]\) e derivabile in \((a,b)\). Allora esiste \(c \in (a,b)\) tale che \(\frac{f(b)-f(a)}{b-a}=f'(c)\).

Ricordando l’interpretazione geometrica della derivata prima come coefficiente angolare della retta tangente, si può avere una visualizzazione grafica dell’enunciato di questo teorema. Infatti questo garantisce, sotto le ipotesi di continuità e derivabilità, l’esistenza di un punto \(c\in (a,b)\) tale per cui la retta tangente al grafico della funzione nel punto \((c,f(c))\) è uguale al coefficiente angolare della retta passante per i punti \((a,f(a))\) e \((b,f(b))\), come in figura.

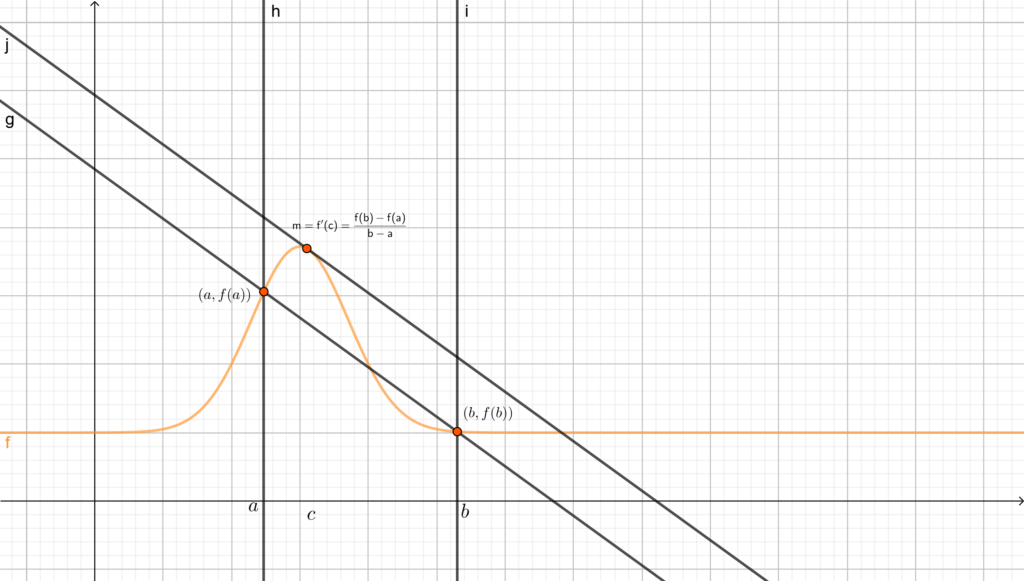
Tornando in autostrada, cerchiamo di sfruttare questo teorema utilizzando come \(f\) la nostra funzione \(x:[t_1,t_2]\to \mathbb{R}\), supponendo che essa sia continua su \([t_1,t_2]\) e derivabile su \((t_1,t_2)\). Il significato dell’assunzione della continuità e della derivabilità della funzione posizione è che nel nostro moto effettivamente non possano esserci movimenti troppo bruschi.

Sotto queste ipotesi si può applicare il teorema di Lagrange, che garantisce che esiste almeno un istante \(t* \in (t_1,t_2)\) tale per cui \(v(t*)=x'(t*)=\frac{x(t_1)-x(t_2)}{t_1-t_2}=v_m\). Pertanto \(v(t*)=v_m\): dunque nell’istante \(t*\) (non sappiamo quale istante sia ma siamo sicuri che esista) la velocità istantanea \(v(t*)\) è uguale alla velocità media \(v_m\) registrata dal Safety Tutor, che risulta essere maggiore al limite di velocità \(L\). Non abbiamo scampo dunque, e ci arriverà a casa una multa.

Il problema è stato risolto grazie al teorema di Lagrange, ma c’è un’altra problematica a cui il Safety Tutor non pone rimedio. Infatti il fatto che la velocità media \(v_m\) sia inferiore a \(L\) non garantisce che non ci sia stato un istante \(t*\) in cui la nostra velocità istantanea fosse superiore al limite. Facciamo un esempio.

Per comodità supponiamo \(t_1=0\) e \(x_1=x(t_1)=0\), cosa che possiamo sempre fare a meno di cambiare il sistema di riferimento.

La nostra legge oraria (esprimendo il tempo in ore e lo spazio in kilometri) nel tratto \([0,t_2]\) è la seguente: \(x(t)=-240t^2+240t\), supponendo che \(t_2\) registrato dal Tutor sia \(t_2=0,5\).

Osserviamo che si tratta di una legge oraria sensata nell’intervallo \([0,0.5]\) perchè in questo intervallo la funzione \(x(t)\) è sempre crescente, in accordo con l’evidenza che in autostrada non si può tornare indietro.

La velocità media rilevata dal Tutor è \(v_m=\frac{x(0,5)-x(0)}{0,5-0}={60-0}{0,5}=120 km/h < L\).

Dunque, se il limite di velocità è \(L=130 km/h\). la nostra velocità media è inferiore al limite e non prendiamo la multa, anche se abbiamo fatto i furbi: in effetti nell’istante \(t*=0,125 (h)\) la nostra velocità istantanea è stata \(x'(t*)=-480t*+240=180 km/h\), ben oltre il limite \(L\). Forse il grafico chiarirà ancor più le idee.

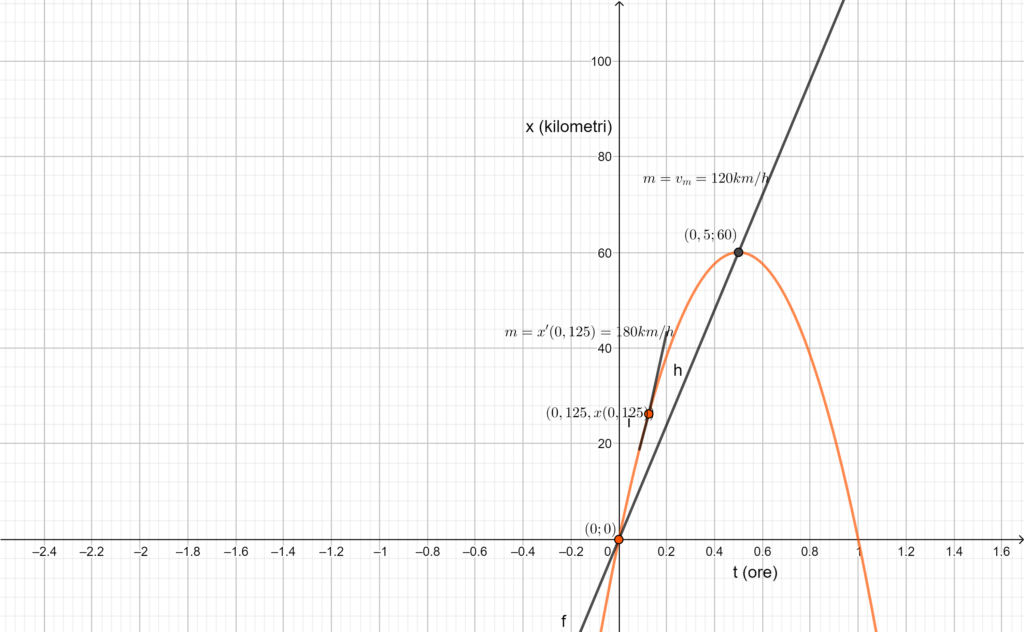
L’unico modo per ovviare a questo problema è quello di avvicinare sempre di più le stazioni di rilevamento, in modo che la velocità media sia sempre più assimilabile alla velocità istantanea: in effetti è quello che accade con gli autovelox, dove è presente addirittura una sola torretta, con due rilevatori a distanza di pochi centimetri.

Ecco come Lagrange vi spiega il motivo per cui prendete una multa  😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!