I numeri complessi

Che cosa sono i numeri complessi?

Oggi parleremo di questo insieme numerico, spiegando il motivo per cui si è resa necessaria la sua introduzione e scoprendo come possono essere rappresentati i suoi numeri.

L’insieme numerico

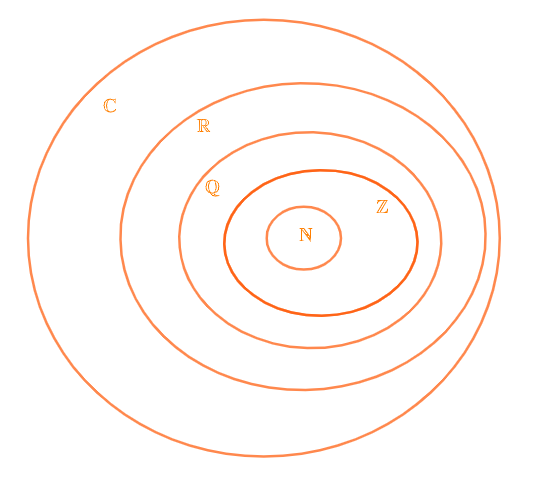
La nascita di un nuovo insieme numerico che estenda un insieme già utilizzato è la logica conseguenza dell’impossibilità, all’interno di esso, di effettuare tutte le operazioni. Facciamo qualche esempio: 

•  All’interno dell’insieme dei numeri naturali \(\mathbb{N}\) (1,2,3,…) non si possono efffettuare tutte le sottrazioni (ad esempio \(2-3\)). Ecco che nasce l’insieme dei numeri interi \(\mathbb{Z}\).
• All’interno di \(\mathbb{Z}\) non si possono effettuare tutte le divisioni (ad esempio \(-2/3\)). Questo giustifica il passaggio all’insieme dei numeri razionali \(\mathbb{Q}\).
• All’interno di \(\mathbb{Q}\) non si possono effettuare tutte le estrazioni di radice (ad esempio \(\sqrt{2}\)). Da qui la nascita di \(\mathbb{R}\), insieme dei numeri reali.                            

Tuttavia anche all’interno dei numeri reali non è lecito compiere qualsiasi operazione. Come ben sapete, infatti, non è possibile estrarre la radice quadrata di un numero negativo! Per ovviare a questo problema, si estende l’insieme dei numeri reali a un insieme più ampio, dove ciò è lecito. Si tratta dell’insieme dei numeri complessi, indicato con \(\mathbb{C}\).

La struttura algebrica

L’insieme dei numeri complessi contiene numeri che possono essere identificati da una coppia ordinata di reali \((a,b)\): a questa coppia corrisponde un numero complesso che indichiamo con la scrittura \(a+ib\). Una domanda vi sorgerà spontanea: cos’è questa i?

La i si chiama unità immaginaria, ed è definita come \(i=\sqrt{-1}\). Effettivamente questa scrittura, che non ha senso in \(\mathbb{R}\), acquista un suo significato in \(\mathbb{C}\), e il suo significato sta proprio in questo particolare numero complesso. Elevando al quadrato l’espressione scritta precedentemente, possiamo anche concludere che \(i^2=-1\).

Avendo chiarito il concetto dell’unità immaginaria, possiamo concludere che tutti i numeri complessi si possono scrivere nella forma \(z=a+ib\), con \(a\) e \(b\) numeri reali. Definiamo \(a\) la parte reale di z, mentre \(b\) la parte immaginaria di z. (Attenzione: non lasciamoci confondere dal nome! La parte immaginaria b è un numero reale, da non confondere con ib. Infatti la parte reale e la parte immaginaria sono due numeri reali, quelli di cui si parlava all’inizio del paragrafo).

Andiamo ora a definire le operazioni in questo insieme, così da dargli una struttura algebrica. Siano ad esempio \(z=a+ib\) e \(w=c+id\) due numeri complessi. Definiamo quindi

• la somma \(z+w=(a+c) +i(b+d)\) cioè il numero complesso avente come parte reale \(a+c\) e come parte immaginaria \(b+d\), che quindi è identificato dalla coppia di numeri reali \((a+c,b+d)\).
• il prodotto \(zw=(a-d)+i(b+c)\) , con parte reale \(a-d\) e parte immaginaria \(b+c\),  identificato dalla coppia di numeri reali \((a-d,b+c)\).

Se la definizione del prodotto di due numeri complessi potrà sembrarvi strana e meno intuitiva di quella della somma, potrete convincervi della sua sensatezza provando a svolgere “a mano” il prodotto \((a+ib)(c+id)\), supponendo valga la proprietà distributiva e ricordandosi che \(i^2=-1\).

Il piano di Gauss e la forma trigonometrica

Il fatto che ogni numero complesso si possa identificare con una coppia di numeri reali \((a,b)\) porta con sè la naturale conseguenza che l’insieme dei numeri complessi possa essere rappresentato su un piano cartesiano, che sull’asse delle x rappresenta la parte reale e sull’ase delle y quella immaginaria. Vediamo ad esempio come i numeri complessi \(z_1=-2+3i\), \(z_2=2=2+0i\) e \(z_3=3i=0+3i\) si rappresentano nel piano di Gauss.

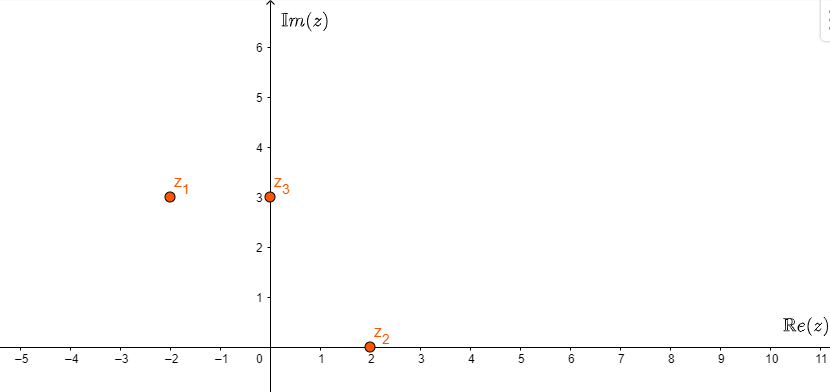
Il piano di Gauss ci ha permesso di trovare un secondo modo di identificare i numeri complessi: oltre a una coppia di numeri reali, possono essere visti come punti del piano. Tuttavia esiste un terzo modo per classificare gli elementi di \(\mathbb{C}\), e deriva dal fatto che ogni punto del piano(ad eccezione dell’origine degli assi) può essere descritto, oltre che dalle sue coordinate cartesiane (ascissa e ordinata), anche delle sue coordinate polari.

Consideriamo ad esempio \(z_1=-2+3i\) come punto del piano di Gauss. Questo è univocamente determinato dalla sua distanza dall’origine (che indichiamo con \(\varrho\)) e dall’angolo orientato compreso fra il semiasse positivo delle x e la semiretta passante per l’origine del piano di Gauss e \(z_1\) (che indichiamo con \(\vartheta\)). 

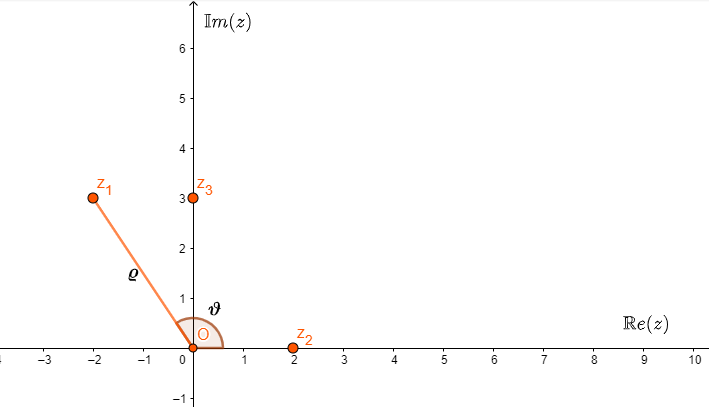
Utilizzando questa notazione ci accorgiamo che, usando la trigonometria

\(a=\varrho \cos{\vartheta}\) e \(b=\varrho \sin{\vartheta}\)

Usando questa scrittura possiamo scrivere un numero complesso nella forma

\(z=\varrho(\cos{\vartheta}+isin{\vartheta})\)

, che è la forma trigonometrica di un numero complesso. Viceversa, data la forma algebrica \(z=a+ib\) è possibile passare a quella trigonometrica in questo modo (sempre usando la trigonometria):

\(\varrho=\sqrt{a^2+b^2}\) e \(\vartheta=\arctan{\frac{b}{a}}\)

Attenzione! Nel calcolo dell’angolo sto supponendo che \(a\ne0\), perchè altrimenti non avrebbe senso la frazione (è vero che nell’insieme dei numeri complessi cose strane come la radice quadrata di un numero negativo hanno senso, ma scrivere uno zero al denominatore è comunque sbagliato!). Nel caso appena citato, infatti l’angolo \(\vartheta\) vale \(\frac{\pi}{2}\) (nel caso in cui \(b>0\) come per \(z_3\)) oppure \(\frac{3}{2} \pi\) (se \(b<0\)). L’unico caso non analizzato è quello in cui \(a=b=0\), in cui però le coordinate polari non sono ben definite (in quanto, appunto, non si può determinare l’angolo).

Con un semplice esercizio vediamo ora come si passa dalla forma algebrica a quella trigonometrica.

Esercizio Scrivere il numero complesso \(z=1+i\) in forma trigonometrica. 

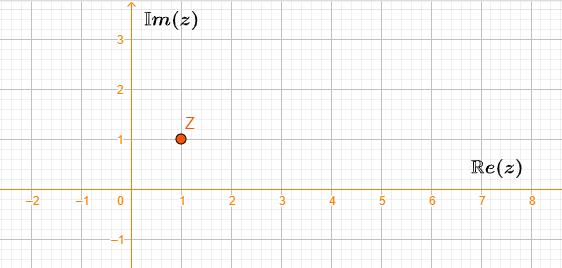
Per risolvere questo esercizo dobbiamo concentrarci sull’identificazione della prima coordinata trigonometrica: \(\varrho\). Questa è semplice da calcolare, perchè si può subito notare che sia la parte reale sia la parte immaginaria di \(z\) valgono \(1\). Dunque possiamo scrivere

\(\varrho=\sqrt{1^2+1^2}=\sqrt{2}\).

Volendo arrivare a una scrittura del tipo \(z=\varrho(\cos{\vartheta}+i\sin{\vartheta})\) raccolgo \(\varrho=\sqrt{2}\) alla forma algebrica di \(z\).

Ottengo quindi 

\(z=\sqrt{2}(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i)\).

E razionalizzando 

\(z=\sqrt{2}(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i)\).

Per completare l’esercizio devo trovare quell’angolo \(\vartheta\) tale per cui 

\(\cos{\vartheta}=\frac{\sqrt{2}}{2}\) e

 
\(\sin{\vartheta}=\frac{\sqrt{2}}{2}\).

Dalla trigonometria sappiamo che questo angolo è \(\vartheta=\frac{\pi}{4}\). Perciò possiamo concludere che

\(z=1+i=\sqrt{2}(\cos{\frac{\pi}{4}}+i\sin{\frac{\pi}{4}})\).

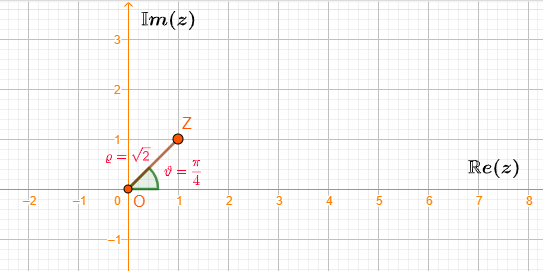
Siamo quindi passati dalla forma algebrica a quella trigonometrica.

Queste erano alcune nozioni base riguardo ai numeri complessi! 😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!