Funzione “sinuosa”

Gli appunti di oggi trattano un esercizio di studio di funzione: si cercheranno di studiare le caratteristiche di una funzione particolarmente “sinuosa”.

In figura è riportato il grafico della funzione \(f(x)=x+\sin{x}\).

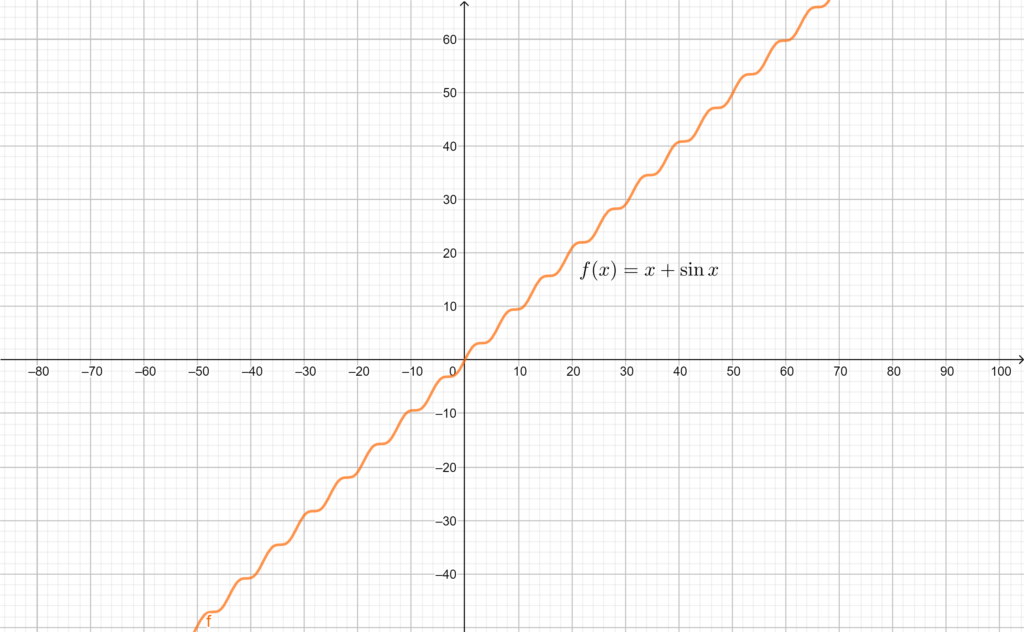
Si calcolino i limiti della funzione agli estremi del suo dominio e si stabilisca se il grafico ammette o meno asintoti di qualunque genere.

Osservando il grafico della funzione, è chiaro che i limiti di \(f\) per \(x\to \pm \infty\) saranno \(\pm \infty\), ma mostrarlo con precisione non è così scontato! Infatti, volendo risolvere ingenuamente questo limite, incapperemmo in una problematica:

\(lim_{x\to +\infty} x+\sin{x}=+\infty+sin({+\infty})\).

Qual è il problema? Il problema è che \(\sin{x}\) non ammette limite per \(x\to\infty\): è noto, infatti, che si tratta di una funzione che oscilla tra \(-1\) e \(1\) con periodo \(2\pi\). Un buon metodo per risolvere questo problema e mostrare, come ci aspettiamo, che tale limite è \(+\infty\), è appellarsi al teorema del confronto. Se mostrassimo che \(f(x)=x+\sin{x}\) è sempre maggiore di una funzione il cui limite per \(x\to +\infty\) è \(+\infty\), il teorema del confronto ci garantirebbe che \(lim_{x\to +\infty} x+\sin{x}=+\infty\).

Osservando che \(\sin{x}\ge -1 \,\,\forall x\in\mathbb{R}\), concludiamo che:

\(f(x)=x+\sin{x}\ge x-1 \,\, \forall x\in\mathbb{R}\).

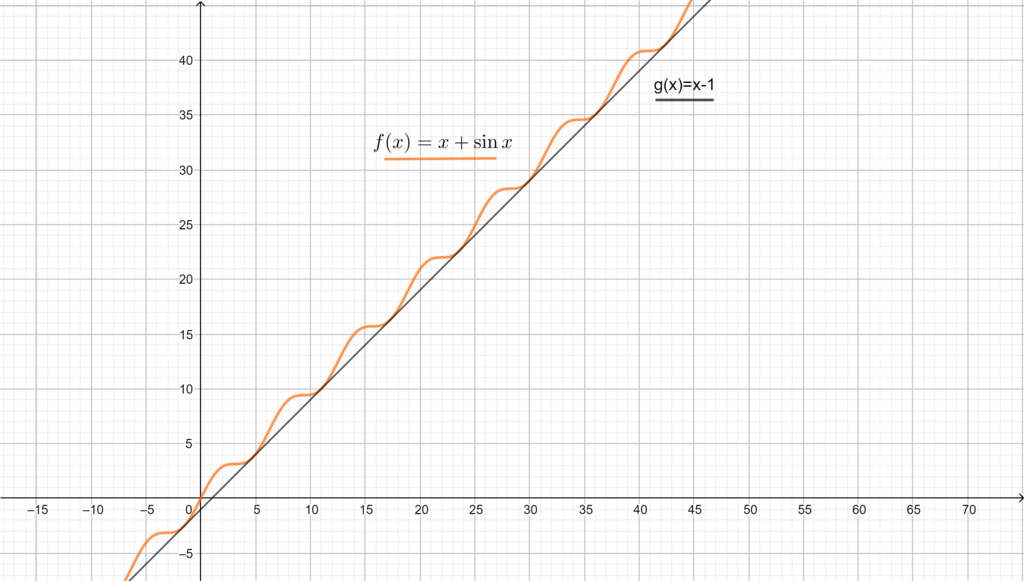
In base al teorema del confronto, allora \(\lim_{x\to +\infty}f(x)\ge \lim_{x\to +\infty} x-1= +\infty\). Dunque
\(\lim_{x\to +\infty}f(x)=+\infty\), come ci aspettavamo.

Per quanto riguarda \(\lim_{x\to -\infty}f(x)\), essendoci le stesse problematiche, ragioniamo in maniera analoga: questa volta mostriamo che \(f(x)\) è sempre minore di una funzione il cui limite per \(x\to -\infty\) è \(-\infty\). Poichè \(\sin{x}\le 1 \,\, \forall x\in\mathbb{R}\), allora

\(f(x)=x+\sin{x}\le x+1\) \(\forall x\in\mathbb{R}\).

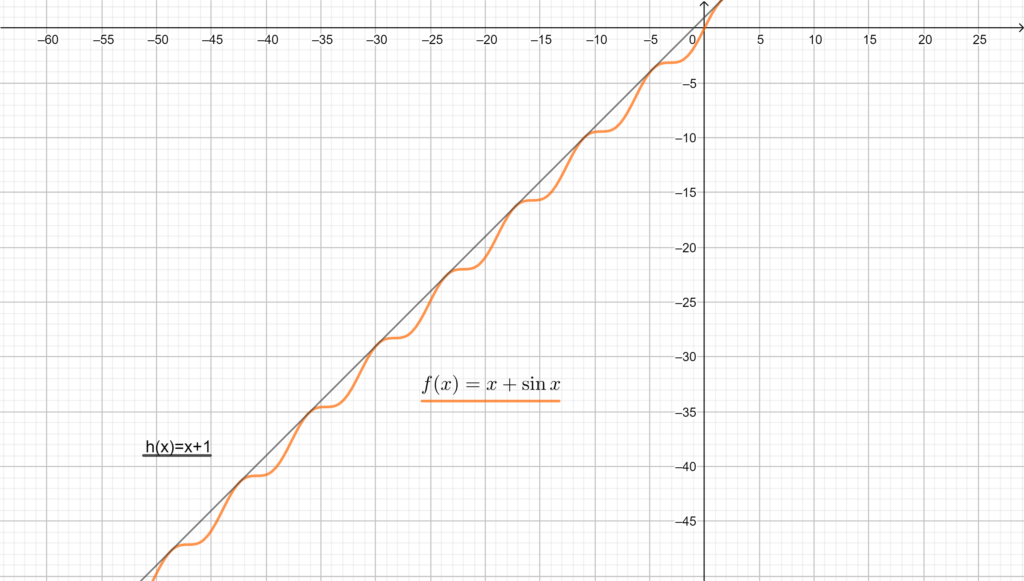
In base al teorema del confronto \(\lim_{x\to -\infty}f(x)\le \lim_{x\to -\infty} x+1= -\infty\). Perciò \(\lim_{x\to -\infty}f(x)=-\infty\).

Passiamo ora agli asintoti: è chiaro che il fatto che la funzione sia continua su \(\mathbb{R}\) e che i limiti a \(\pm \infty\) siano infiniti escludono le possibilità che ci siano asintoti verticali e orizzontali. Resta da analizzare la presenza o meno di asintoti obliqui.

Dobbiamo controllare due ulteriori condizioni (lo facciamo solo per \(x\to +\infty\)).

1. \(\lim_{x\to +\infty} \frac{f(x)}{x}=m\in\mathbb{R}\setminus \{0\}\). Questa \(m\) sarà il coefficiente angolare dell'(eventuale) asintoto obliquo.
2. \(\lim_{x\to +\infty} f(x)-mx=q\in\mathbb{R}\). La \(q\) risulterà essere il termine noto dell’asintoto obliquo

Per quanto riguarda la condizione 1., la risoluzione del limite è, ancora una volta, scomoda per via della presenza della sinuosità del seno. In effetti

\(\lim_{x\to +\infty} \frac{x+\sin{x}}{x}= \frac{+\infty+sin(+\infty)}{+\infty}\)

, che ancora una volta presenta l’inconveniente della non esistenza del limite del seno. Si utilizzerà ancora una volta il teorema del confronto, però in quella forma che è nota a tutti con il nome più figurativo di teorema dei due carabinieri. Questo limite sembra proprio fare \(1\), perchè \(\frac{f(x)}{x}\) può essere scritto come \(1+\frac{\sin{x}}{x}\), vale a dire \(1\) più una quantità che, per quanto oscillante, vede il numeratore soccombere sul denominatore quando \(x\to +\infty\). Per giustificare questo passaggio bisogna cercare due funzioni \(g_1(x),g_2(x)\) tali per cui \(g_2(x)\le f(x)\le g_1(x)\) in un intorno di \(+\infty\) e

\(\lim_{x\to +\infty}g_1(x)=\lim_{x\to +\infty}g_2(x)=1\), così che le due funzioni, come due carabinieri, forzino anche \(f(x)\) ad avere limite \(1\). Le disuguaglianze, come al solito, si trovano partendo da \(-1\le\sin{x}\le1\), dunque per ogni \(x>0\) vale

\(1-\frac{1}{x}\le \frac{f(x)}{x}=1+\frac{\sin{x}}{x}\le 1+\frac{1}{x}\) per ogni \(x>0\).

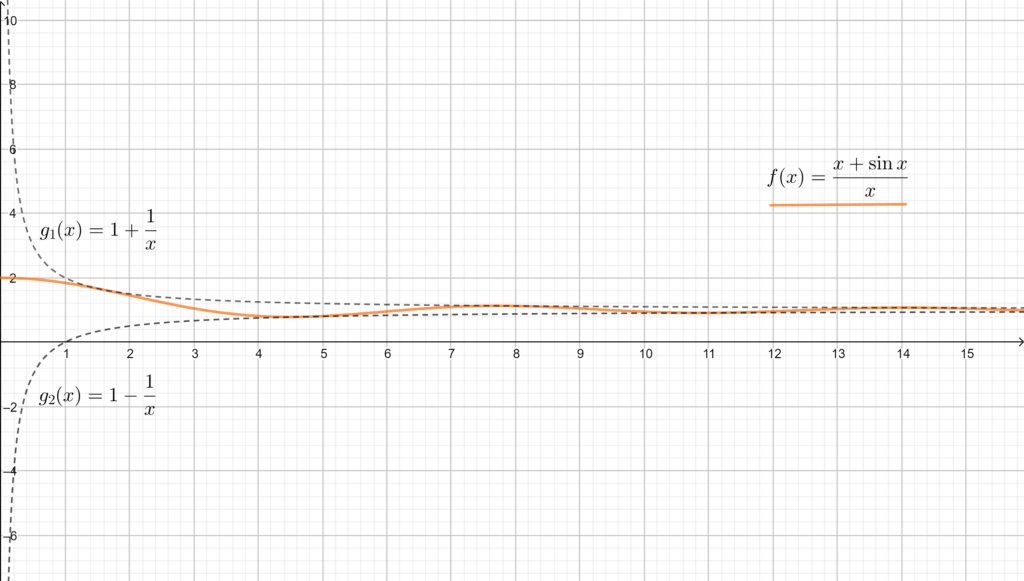
Dunque, come si osserva anche in figura, il teorema dei due carabinieri garantisce che

\(1=lim_{x\to +\infty} 1-\frac{1}{x}\le lim_{x\to +\infty} \frac{f(x)}{x} \le lim_{x\to +\infty} 1+\frac{1}{x}=1\).

Dunque \(lim_{x\to +\infty} \frac{f(x)}{x}=1\): perciò, se la nostra funzione ammettesse asintoto obliquo per \(x\to +\infty\), allora questo asintoto avrebbe coefficiente angolare \(1\).

Dobbiamo andare ora a controllare la condizione 2, stabilendo se è vero che \(lim_{x\to +\infty} f(x)-mx=q\in\mathbb{R}\). In caso affermativo, questa \(q\) sarebbe il termine noto del nostro asintoto obliquo.

Tuttavia, andando a svolgere il limite (e ricordando che nel nostro caso \(m=1\)), si ha

\(\lim_{x\to +\infty} x+\sin{x}-x=\lim_{x\to +\infty}\sin{x}\).

Tuttavia questo non esiste! (Come già osservato). Questo significa che \(f(x)\), nonostante la condizione 1 fosse verificata, non ammette asintoto obliquo. Il significato geometrico di questo fatto è che la nostra funzione va all’infinito complessivamente come una retta con coefficiente angolare \(1\), ma per via della sua sinuosità oscilla continuamente tra rette diverse, senza “sceglierne” una. La seguente immagine, forse, può essere esplicativa.

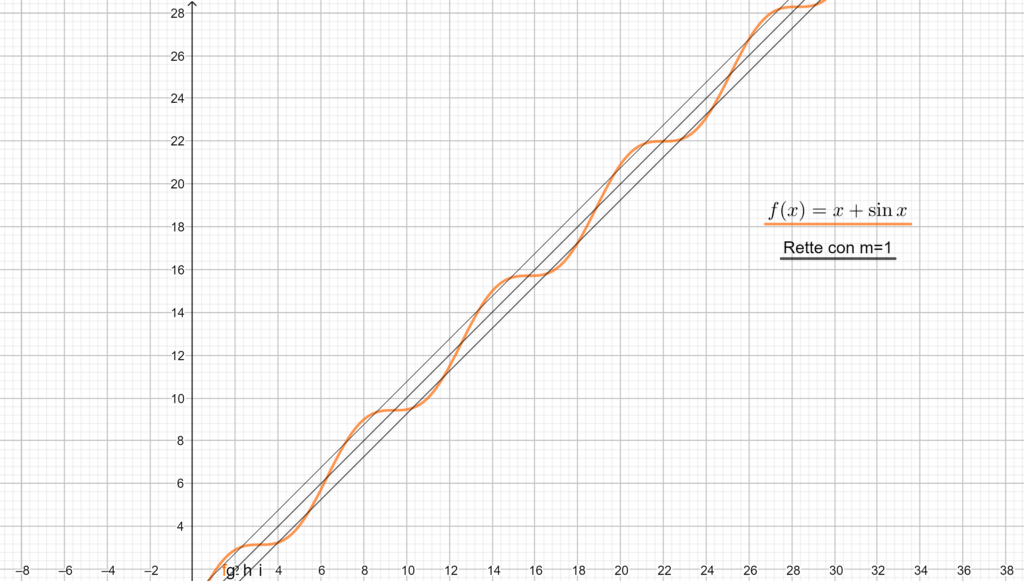
Per esercizio il lettore può svolgere il calcolo dell'(eventuale) asintoto obliquo per \(x\to -\infty\).

Dimostra che il grafico della funzione ammette infiniti punti di flesso, per i quali si devono determinare le coordinate. Inoltre si osservi che questi sono tutti allineati: si determini l’equazione della retta a cui appartengono.

Dal grafico sembrerebbe che i punti di flesso sono di natura eterogenera: a tangente orizzontale e a tangente obliqua.

1. FLESSI A TANGENTE ORIZZONTALE

Prima di tutto andiamo a studiare il segno e gli zeri della derivata prima di \(f(x)\), per cercare i punti di flesso a tangente orizzontale.

\(f'(x)=1+\cos{x}\). Poichè \(\cos{x}\ge -1 \Rightarrow f'(x)\ge 0\) \(\forall x\in\mathbb{R}\). Dunque la funzione sarà monotona crescente: questo garantisce che non sono ammessi estremanti relativi (massimi e minimi relativi), quindi gli unici punti stazionari saranno punti di flesso a tangente orizzontale. Quali sono questi punti? Andiamo a risolvere

\(f'(x)=1+\cos{x}=0 \Rightarrow \cos{x}=-1\). Si sa che gli unici punti il cui coseno è \(-1\) sono quelli del tipo

\(x_k=(2k+1)\pi\), \(k\in\mathbb{Z}\). Dunque sono presenti infiniti punti di flesso a tangente orizzontale, le cui coordinate sono

\(P_k=(x_k,y_k=f(x_k))=((2k+1)\pi,(2k+1)\pi+\sin{(2k+1)\pi}).\) Poichè \(\sin{(2k+1)\pi}=0\), gli infiniti punti di flesso a tangente orizzontale sono \(P_k=((2k+1)\pi,(2k+1)\pi)\).

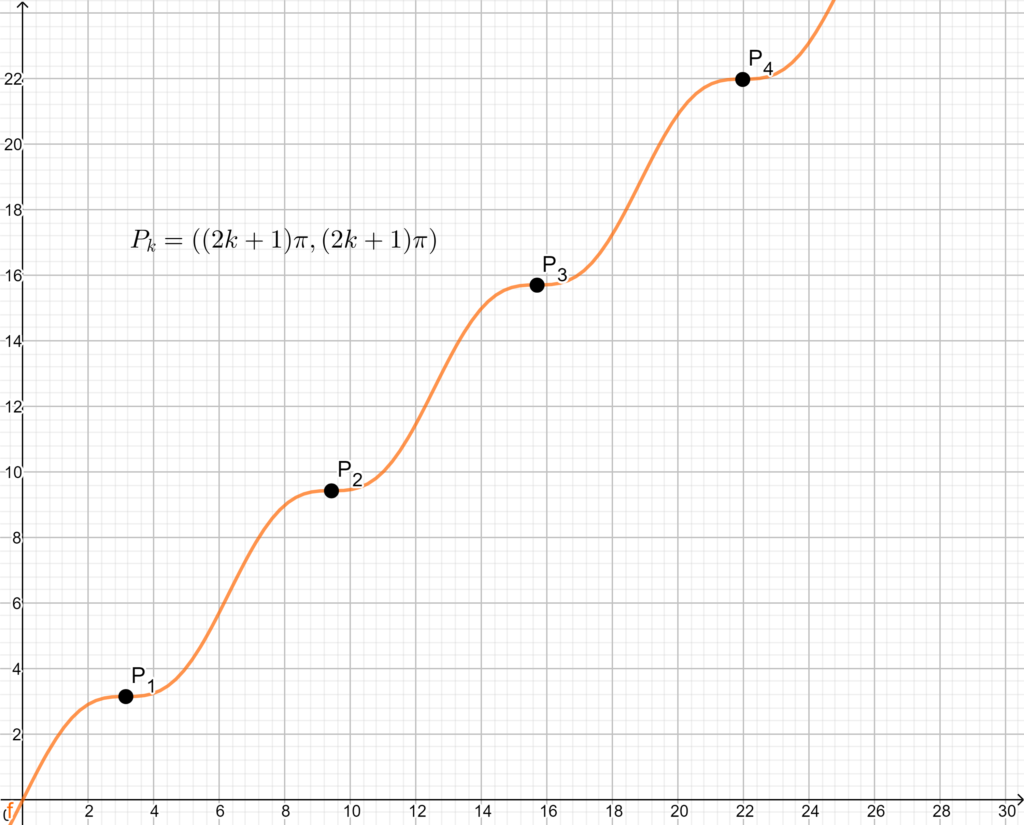
2.PUNTI DI FLESSO A TANGENTE OBLIQUA

Per quanto riguarda gli altri punti di flesso, andiamo a studiare il segno e gli zeri della derivata seconda di \(f\), per capirne la concavità.

\(f”(x)=-\sin{x}\), il cui segno passa periodicamente da positivo a negativo (conseguentemente \(f\) cambia continuamente di concavità): gli zeri di \(f”\), in cui si realizza il cambiamento di concavità, sono punti di flesso.

\(\sin{x}=0 \Rightarrow x_n=n\pi\), \(n\in\mathbb{Z}\). Notiamo che queste \(x_n\) possono essere divise in due insiemi:

• Se \(n\) è dispari abbiamo i punti \(x_k=(2k+1)\pi\), punti di flesso a tangente orizzontale già trovati nel punto precedente.
• Se \(n\) è pari abbiamo i punti \(x_k=2k\pi\), che sono punti di flesso tali per cui la derivata prima \(f'(x_k)=1+\cos{x_k}=2\) non si annulla: quindi la loro tangente non è orizzontale ma obliqua (ha coefficiente angolare \(2\)).

Gli unici non ancora, studiati, quindi, sono quelli del secondo tipo: i punti di flesso a tangente obliqua , che sul grafico di \(f\) (in figura) compaiono come punti del tipo

\(Q_k=(x_k,f(x_k))=(2k\pi,2k\pi+\sin{2k\pi})\Rightarrow\)

\(Q_k=(2k\pi,2k\pi)\).

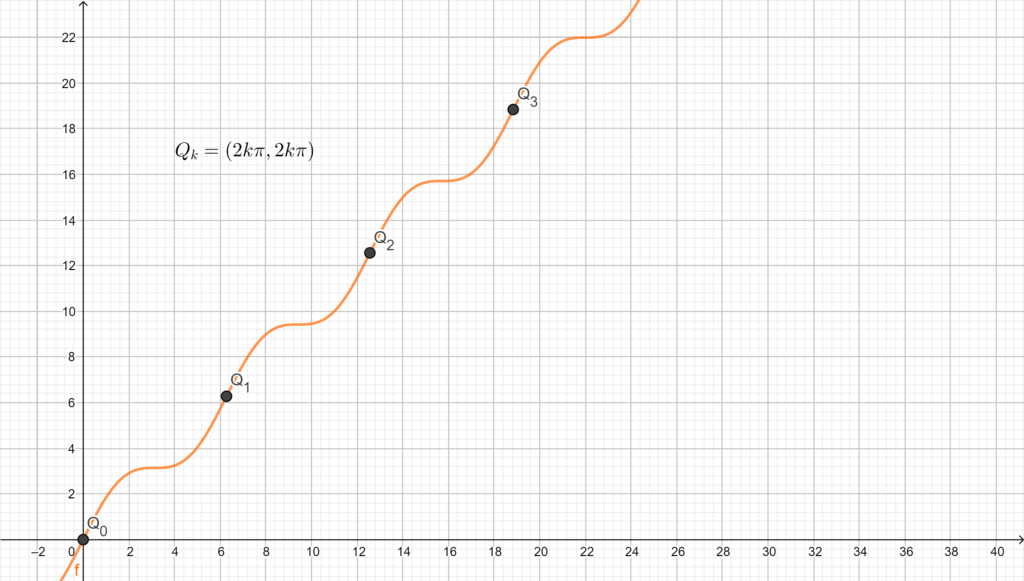
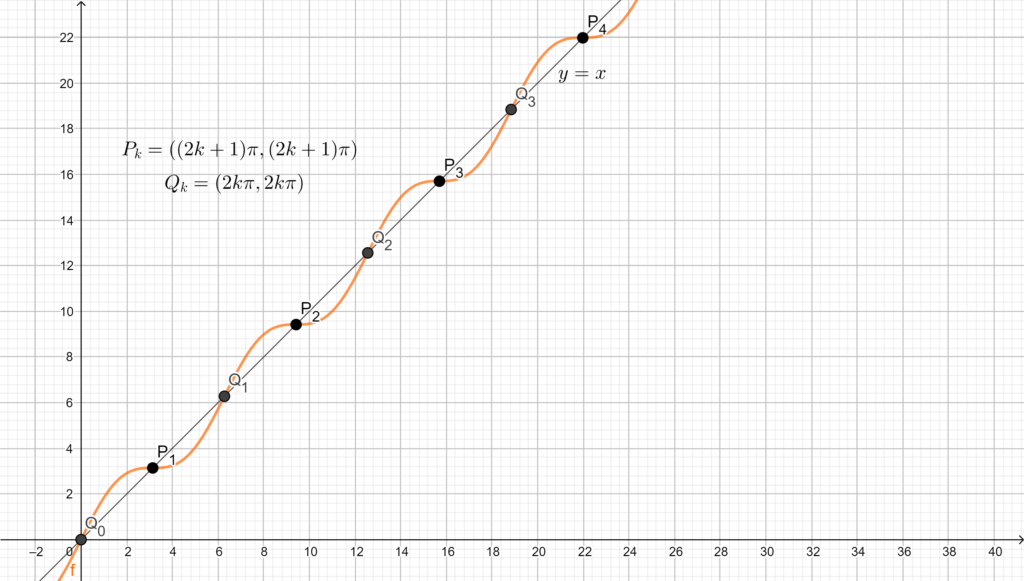
Per concludere, tutti i punti di flesso osservati sono del tipo

• \(P_k=((2k+1)\pi,(2k+1)\pi)\) (tangente orizzontale)
• \(Q_k=(2k\pi,2k\pi)\) (tangente obliqua).

Nonostante la loro diversa tipologia, questi punti hanno la caratteristica di avere l’ascissa uguale all’ordinata: dunque stanno tutti sulla retta

\(y=x\), bisettrice del primo e del terzo quadrante.

Questo era lo studio di una funzione “sinuosa”  😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!