Equazioni differenziali a variabili separabili

Cosa sono le equazioni differenziali a variabili separabili?

In queste pagine di appunti vi forniamo una introduzione liceale allo studio delle equazioni differenziali (ED) del tipo variabili separabili, ossia della forma
\(y’=g(x)\cdot h(y).\)
Cominciamo da un esercizio vero e proprio per poi ricondurci al metodo generale.

Esercizio:

Si determini l’integrale generale (ossia l’insieme di tutte le soluzioni) dell’ED \(y’=2xe^{-y}.\)

Soluzione:

Poiché \(e^{-y} \ne 0 \ \forall y \in \mathbb{R},\) senza problemi riscriviamo l’esercizio come \(y’e^y=2x.\) Possiamo ottenere, osservando che \(y’=\frac{dy}{dx},\)
\(\frac{dy}{dx}e^y=2x \Rightarrow\)
\(e^y dy=2xdx \Rightarrow\)
\(\int e^y \, dy= \int 2x \, dx \Rightarrow\)
\(e^y = x^2 +C, \ C \in \mathbb{R}.\)

Al variare di \(C\) abbiamo condizioni di esistenza che definiscono domini \(D_C\) differenti. In particolare, se \(C>0, D_C=\mathbb{R};\) se \(C\le0\) allora
\(e^y>0 \Rightarrow x^2+C>0 \Rightarrow\)
\(x \in (-\infty , -\sqrt{-C}) \cup (\sqrt{-C}, +\infty) = D_C.\)

Nell’insieme di definizione \(D_C\) è lecito scrivere
\(y(x)=\ln (x^2+C),\)
soluzione dell’esercizio proposto.

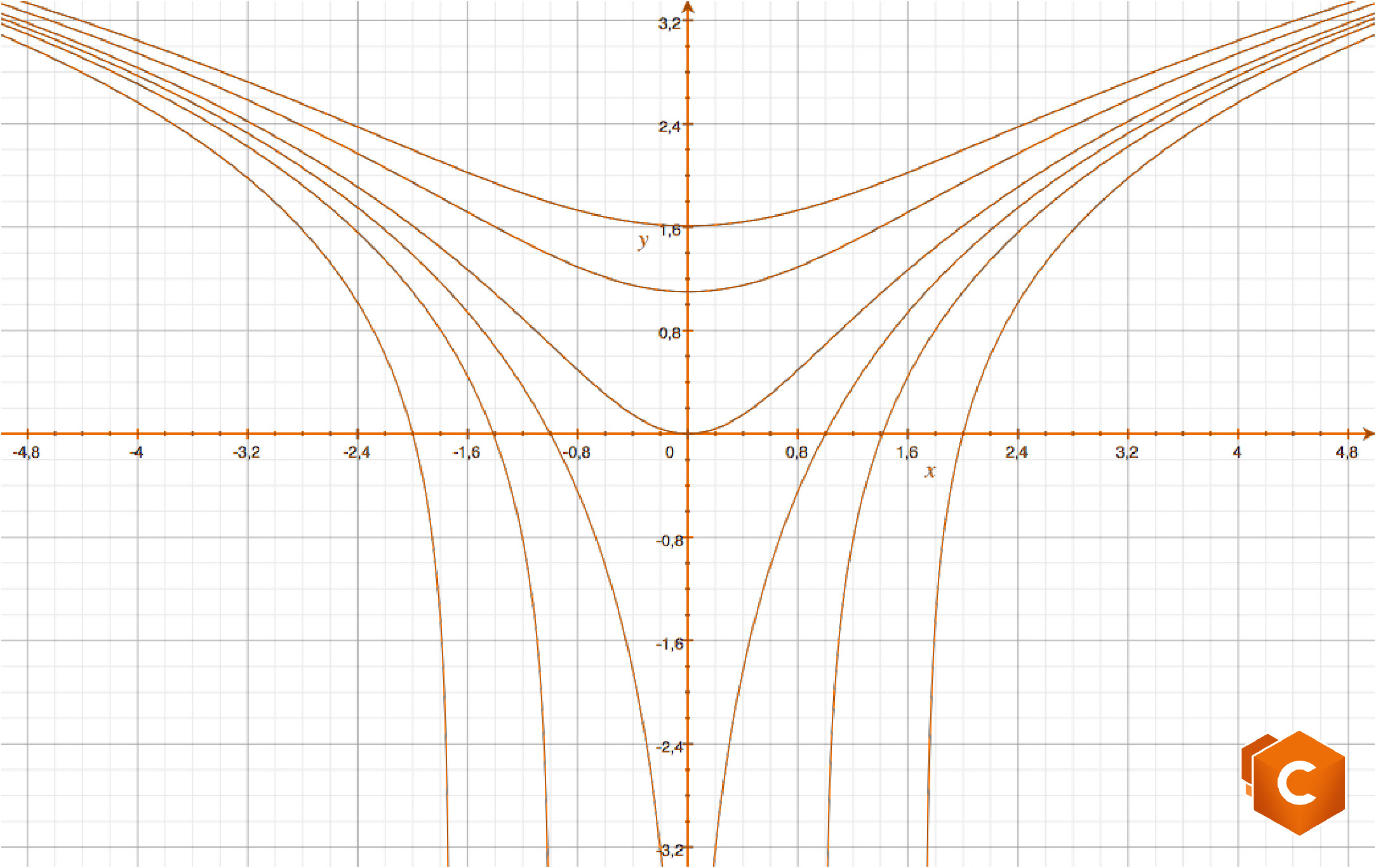
Osservazione 1:

Possiamo notare che, in maniera del tutto analoga a quanto accade nel procedimento di ricerca di una primitiva, la soluzione di un’ED dipende da costanti. In questo esercizio, non solo costanti differenti determinano funzioni differenti, ma anche (in alcuni casi) insiemi di definizione differenti.

Osservazione 2:

Più precisamente quel che abbiamo fatto nei primi passaggi dell’esercizio è dato da:
\(\int e^y \, dy = \int e^{y(x)} y'(x) \, dx =\int 2x \,dx,\)
dove si è supposto di poter operare con il cambio di variabili \(y=y(x).\) A questo punto si procede nell’integrazione come sopra.

Riscriviamo l’esercizio in una forma più generale:
\(y’=g(x)\cdot h(y).\)

In questo esercizio, ad esempio, \(g(x)=2x\) e \(h(y)=e^{-y}.\) Questo caso era piuttosto semplice, poiché \(h(y)\) non si annulla mai. Se per un certo \(\tilde{y}\) vale \(h(\tilde{y})=0,\) allora la funzione costante \(y\equiv \tilde{y}\) è evidentemente (sostituire per credere) soluzione dell’equazione differenziale, definita su tutto \(\mathbb{R}\) (o più precisamente, definita su tutto il dominio di \(g\)). Possiamo quindi riassumere il tutto nella seguente:

STRATEGIA per risolvere un’ED a variabili separabili del tipo \(y’=g(x)\cdot h(y):\)

• Ricercare eventuali soluzioni costanti risolvendo l’equazione \(h(y)=0;\)
• Supporre \(h(y)\neq 0\) (almeno per un punto e quindi almeno per un intervallo – permanenza del segno). Dividere quindi per \(h(y)\) e, scrivendo \(y’ =\frac{dy}{dx},\) ottenere \(\frac{dy}{h(y)}=g(x) \cdot dx;\)
• Concludere l’esercizio integrando membro a membro ed esplicitando (se e dove possibile) \(y.\)

Vediamo all’opera quanto appena detto.

Esercizio:

Risolvere l’ED \(y’-xy+4x=0.\)

Soluzione:

Con un semplice passaggio riportiamo l’esercizio nella forma che ci è più familiare:
\(y’-xy+4x=0 \Rightarrow y’=x(y-4).\)

Risolvendo l’equazione
\(y-4=0 \Rightarrow y=4,\)
deduciamo che \(y\equiv 4\) è (l’unica) soluzione costante. Sia quindi \(y(x) \neq 4\) per qualche \(x \in \mathbb{R}.\) Ricerchiamo \(y(x)\) derivabile e dunque continua; per il teorema di permanenza del segno, esiste un intorno \(U\) di \(x\) in cui \(y(x)\neq 4.\) In tale intorno ha quindi senso dividere per \(y-4.\) Procediamo allora ottenendo
\(\frac{dy}{y-4}=xdx \Rightarrow\)
\(\int \frac{dy}{y-4}=\int x \,dx \Rightarrow\)
\(\ln |y-4| = \frac{x^2}{2} + c,\)
per qualche \(c \in \mathbb{R}.\) Con un passo ulteriore scriviamo
\(|y-4|=e^{\frac{x^2}{2} +c}=e^c e^{\frac{x^2}{2}}.\)
Poiché \(c\) assume un qualsiasi valore in \(\mathbb{R},\) ha senso porre \(c’=e^c,\) ottenendo dunque
\(|y-4|=c’e^{\frac{x^2}{2}},\)
stavolta per qualche \(c’ \in \mathbb{R}, \ c’>0.\) Rimuovendo il valore assoluto, abbiamo
\(y-4=\pm c’e^{\frac{x^2}{2}}.\)
Di nuovo ha senso effettuare un altra sostituzione \(c”=\pm c’,\) nel senso che \(c”\) è una qualsiasi costante in \(\mathbb{R} \setminus \{0\}.\) Segue che
\(y=4+c” e^{\frac{x^2}{2}}.\)
Abbiamo però inizialmente individuato una soluzione costante. Ammettendo che \(c”\) possa essere anche nulla (includendo così anche \(y\equiv 4\)), possiamo ricompattare il tutto in
\(y_C (x)=4+C e^{\frac{x^2}{2}},\)
per qualche \(C \in \mathbb{R},\) famiglia di soluzioni definite su tutto \(\mathbb{R}.\)

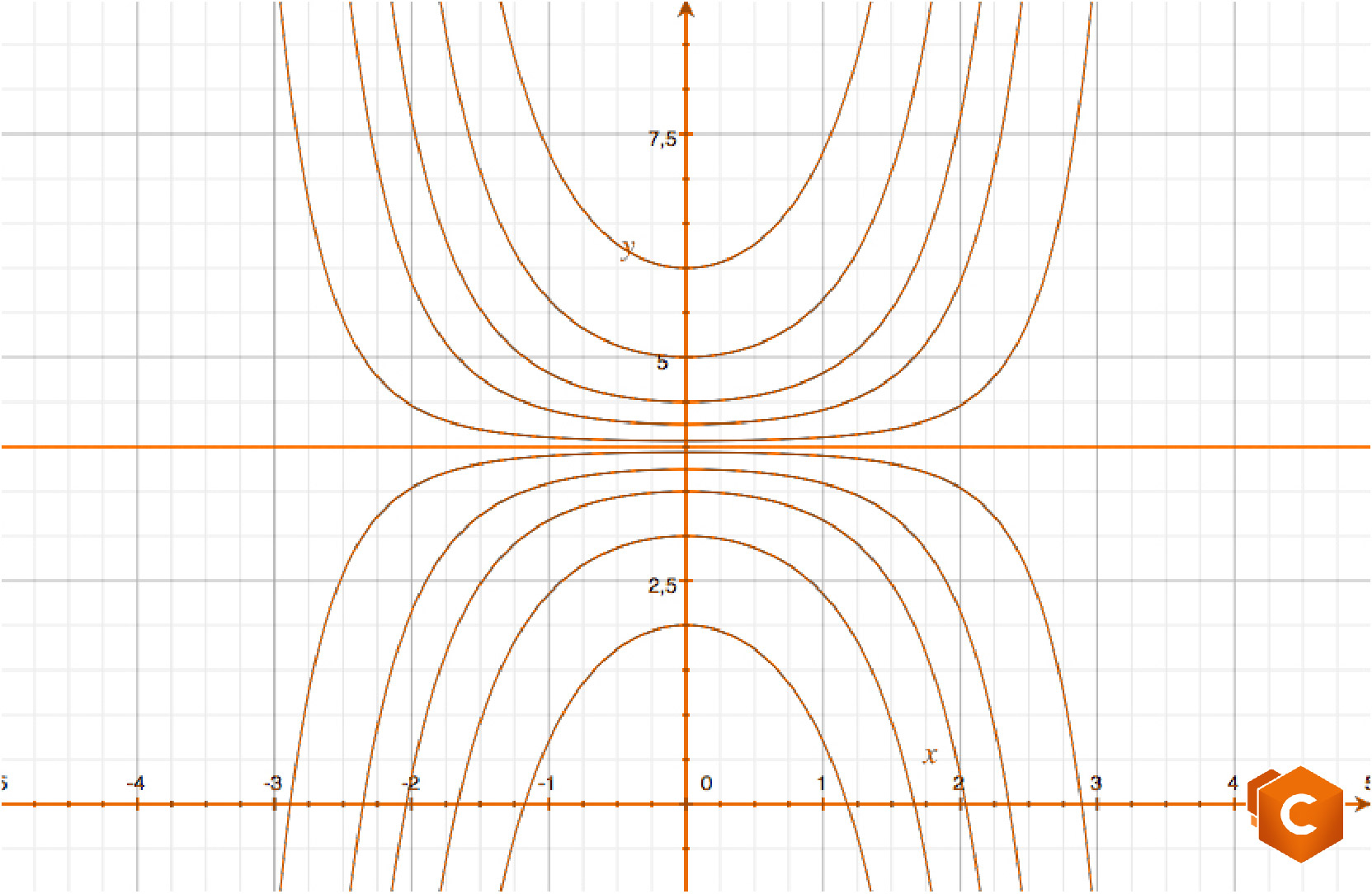
Esercizio:

Risolvere l’ED \(y’=e^x \cos^2 y.\)

Soluzione:

Preoccupiamoci innanzitutto di eventuali soluzioni costanti:
\(\cos^2 y=0 \Rightarrow y = \frac{\pi}{2} + k\pi, \ k \in \mathbb{Z}.\)
Sia dunque \(\cos^2 y(x) \ne 0\) per qualche \(x,\) e dunque per un qualche intorno \(U\) di \(x\) (permanenza del segno assumendo la continuità di \(y(x)\)). Allora in tale intorno possiamo approcciare il problema come una ED a variabili separabili:
\(\frac{dy}{\cos^2 y}=e^xdx \Rightarrow\)
\(\int \frac{dy}{\cos^2 y}=\int e^x \, dx \Rightarrow\)
\(\tan y=e^x +C, \ C \in \mathbb{R}.\)
Esplicitiamo \(y\) nella relazione appena ottenuta, ricordando i possibili inserimenti di periodicità:
\(y (x)=\arctan(e^x + C) + k\pi, \ k \in \mathbb{Z},\)
definite su tutto \(\mathbb{R}.\) A esse vanno aggiunte le soluzioni costanti determinate in precedenza:
\(y \equiv \frac{\pi}{2} + k\pi, \ k \in \mathbb{Z},\)
anch’esse aventi per insieme di definizione tutto \(\mathbb{R}.\)

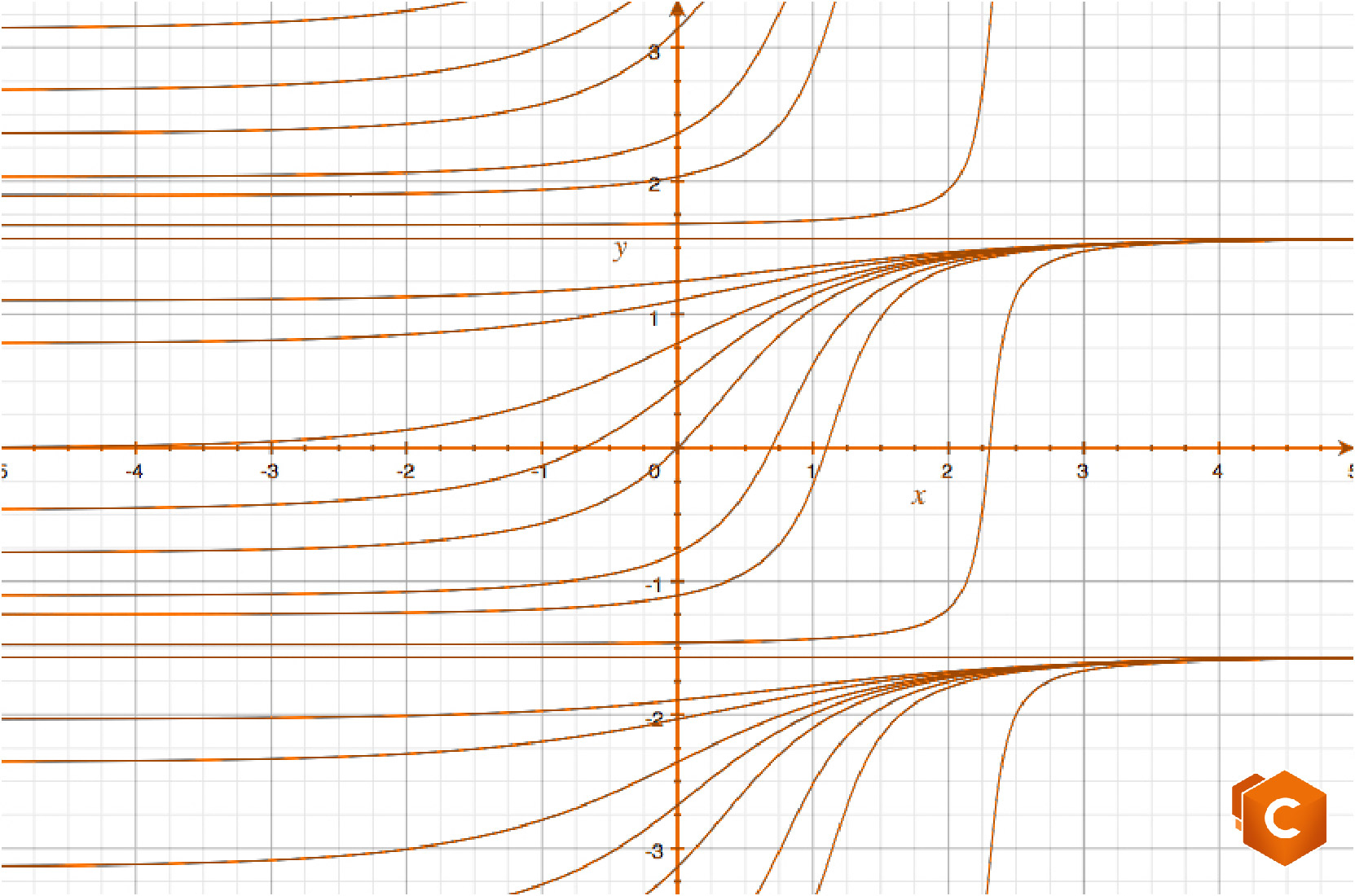
Osservazione 1:

Si osservi che solo a posteriori realizziamo che \(U\) coincide, indipendentemente da \(C\), con \(\mathbb{R}.\) Infatti
\(\cos^2 y(x) = \cos^2(\arctan(e^x +C) + k\pi)=\)
\(\cos^2(\arctan(e^x +C)) \ne 0 \ \forall x \in \mathbb{R},\)
poiché \(\arctan\) è a valori in \((-\pi/2, \pi/2).\)

Osservazione 2:

Questo esercizio presenta un'”anomalia” rispetto alle ED del prim’ordine standard. La soluzione generale, infatti, dipende da due costanti e non da una sola. Notiamo però che una delle due costanti (\(k\)) è a valori discreti e non continui.

Queste erano equazioni differenziali a variabili separabili 😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!