Equazioni di Maxwell

Quali sono le equazioni di Maxwell?

Scopriamolo assieme nelle prossime pagine!

A Maxwell erano note le quattro equazioni

Dal’equazione 1 si può dedurre l’espressione della forza di Coulomb e mostra come il Campo elettrico possa essere prodotto da enti fisici quali cariche elettriche (campo elettrostatico).

L’ equazione 2 esprime la conservatività del campo elettrostatico e da essa può essere dedotta l’espressione del potenziale elettrico e quindi del lavoro elettrostatico. Essa inoltre contiene la legge di Faraday- Neumann-Lenz che mette in evidenza come campi magnetici variabili nel tempo generino un campo elettrico (campo elettromotore) di natura non conservativa.

L’equazione 3 mostra come le linee di campo di B siano sempre chiuse e non esistano monopoli magnetici.

L’equazione 4 mette in evidenza il fatto che le sorgenti di campo magnetico siano le correnti elettriche.

Maxwell nota come vi sia una asimmetria in questo gruppo di equazioni in quanto dalla (1) e dalla (2) si vede che i campi elettrici possono essere generati sia da cariche elettriche che da campi magnetici variabili nel tempo mentre la (4) mostra che le uniche sorgenti di campo magnetico sono invece le correnti.

Oltre a questa considerazione, Maxwell, analizzando un condensatore durante la fase di carica, nota che l’equazione relativa alla circuitazione del campo magnetico lungo il bordo della piastra del condensatore assume valori diversi a seconda che si osservi la piastra da destra o da sinistra

a sinistra infatti avremo 

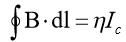
mentre a destra avremo

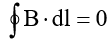
Una stessa situazione fisica non può essere descritta da due equazioni diverse!

Maxwell nota che durante la fase di carica il campo elettrico tra le armature a poco a poco cresce. Aumentando l’intensità di E le molecole del dielettrico si polarizzano sempre di più. questo spostamento di cariche dà origine ad una corrente che Maxwell chiama corrente di spostamento. 

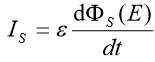
L’equazione della circuitazione di Ampere per il campo magnetico deve dunque essere integrata come segue:

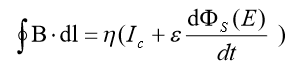
Con l’aggiunta del termine relativo alla corrente di spostamento le equazioni acquistano una nuova simmetria

Campi magnetici variabili nel tempo possano produrre campi elettrici, ma anche campi elettrici variabili nel tempo possano generare campi magnetici.

Dunque se nel caso statico si può parlare di campo elettrico e campo magnetico come due entità fisiche separate, nel caso dinamico, quando è presente un campo elettrico ne compare uno magnetico e viceversa. Non è dunque più possibile parlare di campo elettrico o campo magnetico separatamente, ma dovremo introdurre il concetto di campo elettromagnetico.

Maxwell inoltre ci dice che campi elettrici e magnetici non rimangono confinati nello spazio ma propagano secondo la modalità delle onde, con velocità:

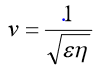
che nel vuoto assume il valore della velocità della luce nel vuoto. Questo risultato suggerisce suggerisce a Maxwell l’idea che la luce sia un’onda di tipo elettromagnetico.

Queste erano le equazioni di Maxwell 🙂 
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!