Coniche

Luoghi geometrici di punti

Un ultimo modo di vedere le coniche è quello di pensarle come luoghi di punti geometrici che soddisfano particolari proprietà. In quest’ottica vanno lette le seguenti definizioni.

DEFINIZIONE:  
La circonferenza è il luogo geometrico dei punti del piano equidistanti da un punto \(C\) detto centro.
La distanza \(r\) dei punti della circonferenza dal centro si dice raggio.

Dunque \(P\) punto del piano appartiene alla circonferenza se e solo se

\(d(P,C)=r.\)

DEFINIZIONE:
La parabola è il luogo geometrico dei punti del piano equidistanti da un punto \(F\), detto fuoco, e da una retta \(d\), detta direttrice.

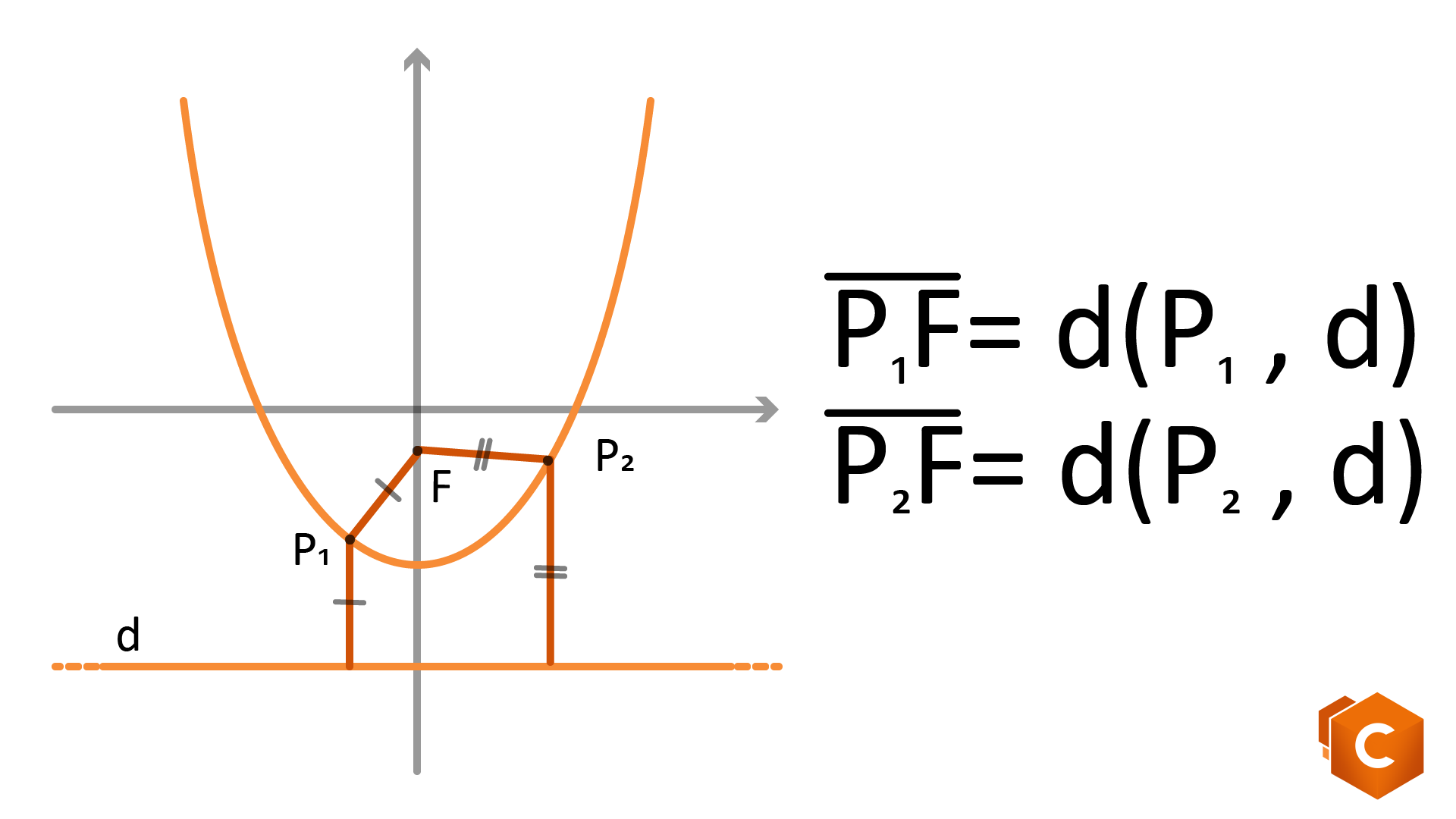
In altri termini, \(P\) punto del piano appartiene alla parabola se e solo se

\(d(P,F)=d(P,r).\)

DEFINIZIONE:
L’ellisse è il luogo geometrico dei punti del piano per cui è costante la somma
delle distanze da due punti fissati \(F_1\) e \(F_2\), detti fuochi.

\(d(P,F_1)+d(P,F_2)=costante.\)

OSSERVAZIONE: Si può notare che, qualora, \(F_1\) e \(F_2\) coincidano, la definizione dell’ellisse è uguale a quella della circonferenza. Infatti, come anticipato in precedenza, la circonferenza può essere considerata come una particolare ellisse.

DEFINIZIONE:
L’iperbole è il luogo geometrico dei punti del piano per cui è costante la differenza
delle distanze da due punti fissati \(F_1\) e \(F_2\), detti fuochi.

\(d(P,F_1)-d(P,F_2)=costante.\)

OSSERVAZIONE: Si può osservare che la definizione dell’iperbole è uguale, a meno di un segno, a quella dell’ellisse.

Queste erano le coniche 😉 
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!