Coniche

Cosa sono le coniche?  

Qui di seguito cerchiamo di spiegartelo fornendoti tre differenti definizioni, ciascuna relativa a un differente punto di vista.

Sezioni di un doppio cono

La prima risposta riflette un punto di vista prettamente geometrico e risponde alla ricorrente domanda: “Perché si chiamano coniche?”.

DEFINIZIONE:
Le coniche sono sezioni piane di un doppio cono.

Si tratta quindi di curve piane che si possono ottenere tagliando un doppio cono con un piano: l’intersezione fra il piano e il doppio cono è una conica.

Ma cos’è un doppio cono? Un doppio cono è il solido ottenibile dalla rotazione di una retta attorno ad un’altra retta verticale (che chiamiamo asse di rotazione) ad essa incidente. Supponiamo, inoltre, che l’angolo tra la retta che abbiamo fatto ruotare e l’asse di simmetria sia \(\theta \).

A seconda dell’angolo formato dal piano con cui viene tagliato e l’asse di rotazione abbiamo diversi tipi di coniche:

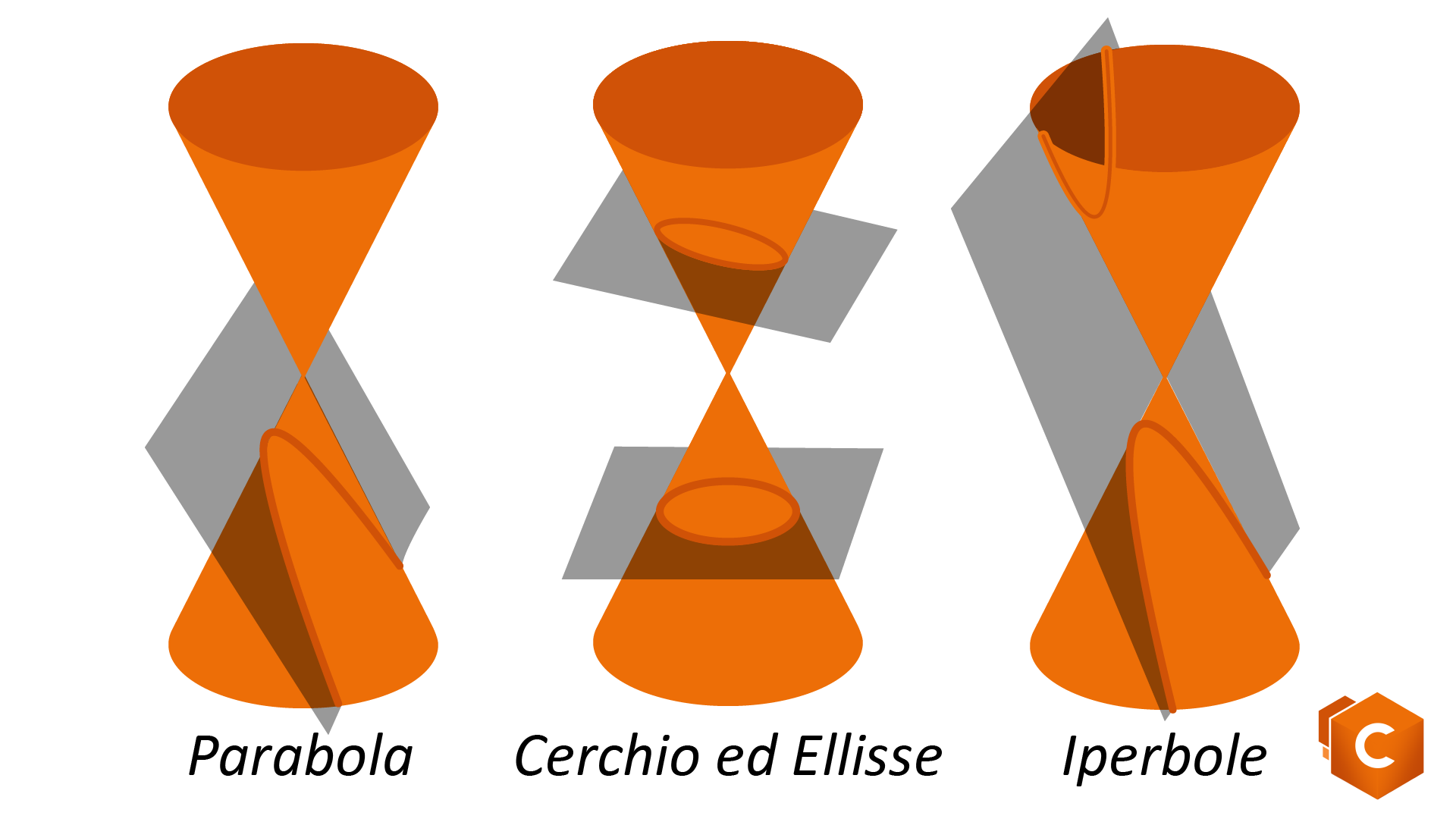
• Parabola se l’angolo formato con l’asse di rotazione è esattamente \(\theta \) ;
• Ellisse se l’angolo formato fra il piano e l’asse è \(\le \pi /2\) o \(> \theta \) ;
• Circonferenza se il piano è perpendicolare all’asse di rotazione (Ricordiamo che la circonferenza è una particolare ellisse!);
• Iperbole se il piano forma con l’asse di rotazione un angolo inferiore a \(\theta\) (in tal caso il piano interseca entrambe le falde del cono, dunque l’iperbole è una conica a due falde).

L’adozione di questa definizione evidenzia anche però la presenza di alcune coniche degeneri. Quando il piano con cui si “affetta” il doppio cono passa per il vertice (punto di intersezione fra l’asse di rotazione del cono e una sua generatrice), ci si trova di fronte ad una delle seguenti situazioni:

• Se il piano è perpendicolare all’asse: l’intersezione è costituita da un solo punto;
• Se il piano è tangente al cono: l’intersezione è costituita da una coppia di rette coincidenti;
• Se il piano forma con l’asse un angolo superiore a \(\theta \) : la sezione è costituita da due rette incidenti.

L’unico caso di conica degenere non considerato in questa prima trattazione è quello di una coppia di rette parallele. Il motivo per cui queste non risultino essere sezioni piane di un doppio cono, però, è abbastanza complesso…

 circonferenza coniche ellisse iperbole parabola