Strette di mano: un esercizio di combinatoria

Avrai sicuramente già visto alcuni esercizi di combinatoria, ma come te la caverai con un problema un po’ più difficile?

Problema. Il testo dell’esercizio in questione è il seguente:

Otto celebrità si incontrano a un party. Succede così che ciascuna celebrità stringe la mano esattamente ad altre due. Un ammiratore tiene una lista di tutte le coppie (non ordinate) di celebrità che si sono strette la mano. Se l’ordine non conta, quante diverse liste sono possibili?

Notiamo subito come sia impossibile applicare immediatamente una semplice formula nota del nostro bagaglio di permutazioni, disposizioni e combinazioni; dovremo quindi lavorare un po’ per poter dare una mano al caro amico paparazzo. Inoltre, vedremo bene come durante la soluzione questo ostico problema proverà più volte a tendere delle trappole al nostro ragionamento.

Soluzione. Prima di tutto cerchiamo un modo per “matematizzare” il problema, ossia reinterpretarlo in un modo più snello e semplice per potervici approcciare in maniera più immediata. Numeriamo le celebrità da \(1\) a \(8\), e immaginiamo di disegnare su un foglio otto punti, anch’essi numerati, in questo modo: cominciamo dalla star numero \(1\) e accanto a lei disegniamo i due vip a cui stringe la mano, e congiungiamo con un segmento due vertici ogniqualvolta c’è una stretta di mano tra le persone corrispondenti. Prima o poi questo grafo dovrà chiudersi, e a questo punto possono succedere due cose:

• Il poligono costruito coinvolge tutte e otto le celebrità: abbiamo finito di disegnare.
• Avanza qualche celebrità: consideriamo il primo tra i festaioli che manca all’appello e costruiamo un nuovo poligono. Di nuovo questo grafo dovrà chiudersi, e a questo punto, per come è costruito il problema, e poiché i presenti sono solo otto, non può avanzare più nessuno (perché?).

Un esempio di situazione che si può presentare è la seguente:

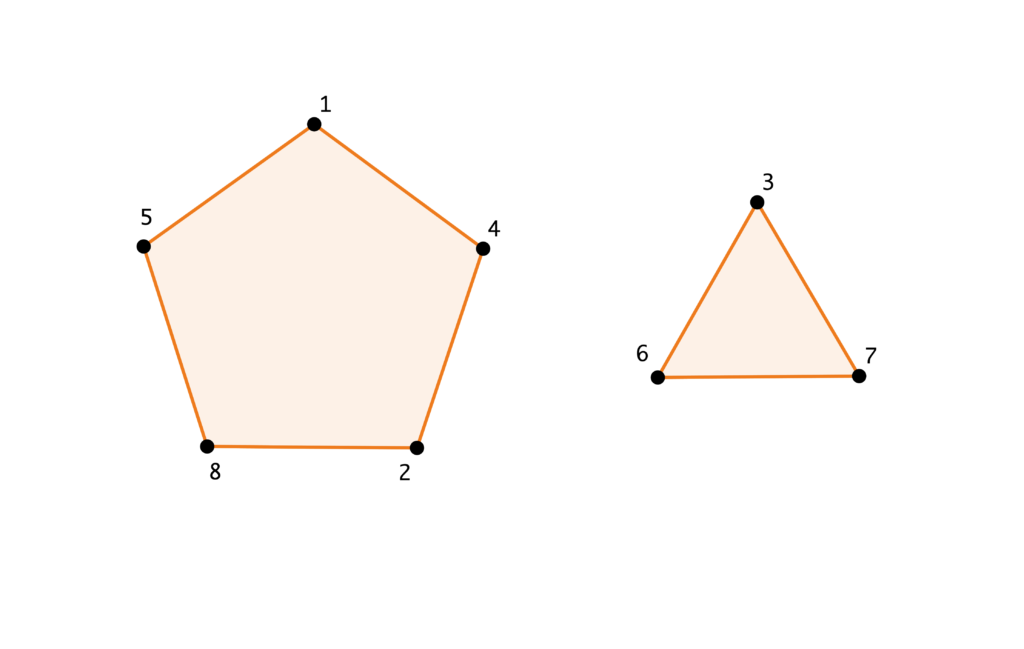
Cominciamo dunque a distinguere i due macro-casi considerati.

Un poligono: un ottagono. Supponiamo che il cerchio si chiuda senza lasciar fuori nessuno: il poligono costruito coinvolge tutti gli otto presenti. In quanti modi può essere costruito? La prima risposta che può venire in mente è semplicemente \(8!\), ma questo risulta il primo (piccolo) tranello teso dall’esercizio: un poligono ottenuto per rotazione da un altro genera una lista equivalente, poiché ognuno stringe la mano esattamente alle stesse persone! (Un po’ come il problema degli invitati seduti attorno a un tavolo, se ne avete già sentito uno simile…) Sembrerebbe quindi che, ogni volta che consideriamo un poligono, ce ne siano \(8\) (compreso lui stesso) che generano la stessa lista. Modifichiamo di poco la risposta e otteniamo quindi \(\frac{8!}{8}=7!\). Ancora questo non basta, e questo è il primo vero sgambetto per cui rischiamo di cadere. Infatti, consideriamo un poligono ottenuto per simmetria da un altro, ossia: la lista di numeri a partire dall’\(1\) letta in senso antiorario nel primo e la lista letta in senso orario nel secondo coincidono. Un esempio è riportato in figura:

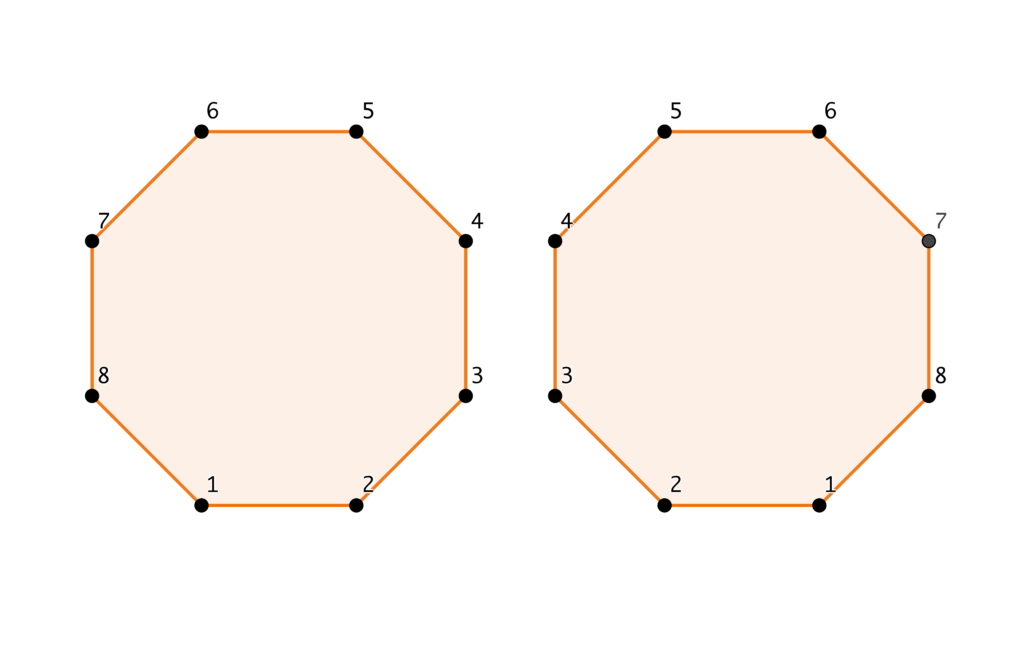
Questi non sono ottenuti per rotazione l’uno dall’altro, come nei casi che abbiamo già considerato, ma generano nuovamente liste uguali (le strette di mano sono le stesse!). Essendoci per ogni poligono un altro ad esso equivalente ottenuto per simmetria, dobbiamo dividere nuovamente per \(2\), ottenendo

\(\frac{8!}{8\cdot 2}=\frac{7!}{2}\).

Due poligoni. Supponiamo ora che il primo cerchio non si chiuda e rimanga fuori qualcuno. Poiché ogni persona stringe la mano ad esattamente altre due, ogni volta che disegniamo un “cerchio”, questo dovrà contenere almeno tre persone. Essendo gli invitati solo otto, segue che al più potremo avere due poligoni! (Poiché \(3+3+3=9>8\)). Potremo quindi costruire o un pentagono e un triangolo, oppure due quadrati. Distinguiamo nuovamente questi due sotto-casi.

Un pentagono e un triangolo. Innanzitutto, dobbiamo decidere come smistare le persone per suddividerle tra i due poligoni. Questo può essere fatto semplicemente utilizzando il coefficiente binomiale \(\binom{8}{5}\), che rappresenta il numero di modi in cui scegliere cinque persone da otto senza che conti l’ordine. Quelle scelte finiranno nel pentagono, quelle escluse nel triangolo. A questo punto ripetiamo il ragionamento fatto in precedenza per l’ottagono, stavolta applicato ai due poligoni: possiamo costruire liste non uguali dal pentagono in \(\frac{5!}{5\cdot 2}=\frac{4!}{2}\) modi, dal triangolo in \(\frac{3!}{3\cdot 2}=1\) modo. Si noti come \(1\) sia un risultato sensato in quanto tre persone possono stringersi le mani in un solo modo, dovendo ciascuna stringer la propria alle altre due. In conclusione, questo sotto-caso ci regala una quantità di configurazioni pari a

\(\binom{8}{5}\cdot \frac{4!}{2}\cdot 1 = \binom{8}{5}\cdot \frac{4!}{2}\).

Due quadrati. Questo caso sembra molto simile al precedente, e potremmo cadere in tentazione rispondendo \(\binom{8}{4}\cdot \frac{3!}{2}\cdot \frac{3!}{2}\) ripetendo un argomento del tutto analogo (il binomiale per smistare, e gli altri due fattori derivanti dalle liste relative ai due quadrati). Qui arriva il trappolone micidiale: dobbiamo dividere per \(2\) un’altra volta. Questo perché, ad esempio, scegliere le persone da \(1\) a \(4\) da posizionare nel primo quadrato ed escludere le altre, quelle da \(5\) a \(8\), inserendole nel secondo, oppure scegliere quelle da \(5\) a \(8\) per il primo quadrato ed escludere le prime, da \(1\) a \(4\), per inglobarle nel secondo, genera situazioni completamente equivalenti! Ciò accade ogni volta che si sceglie un quartetto per il primo dei due quadrati: scegliere il quartetto “opposto” genera situazioni equivalenti! Notiamo come questa circostanza sia sostanzialmente diversa dal caso precedente, perché un pentagono è diverso da un triangolo, ma i due quadrati sono poligoni uguali! In conclusione, questo sotto-caso contribuisce con un numero di modi pari a

\(\binom{8}{4}\cdot \frac{3!}{2}\cdot \frac{3!}{2} \cdot \frac{1}{2}\).

Facendo qualche conticino e sommando il tutto, otteniamo che la soluzione del problema è

\(\frac{7!}{2} + \binom{8}{5}\cdot \frac{4!}{2} +\)
\(+\binom{8}{4}\cdot \frac{3!}{2}\cdot \frac{3!}{2} \cdot \frac{1}{2} =\)
\(=2520 + 56 \cdot 12 +\)
\(+70 \cdot 3 \cdot 3 \cdot \frac{1}{2}=\)
\(= 3507\).

Per i più audaci, vi sfido a ripetere il problema, stavolta con nove celebrità. La soluzione è \(30016\).

Questo era l’esercizio delle strette di mano 😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!