Circuiti elettrici: connessione di bipoli in serie e in parallelo

Cos’è un circuito elementare? Come si può ricondurre un circuito elettrico a un circuito elementare equivalente?

Scopriamolo assieme nelle prossime pagine!

Il più semplice circuito è quello composto dai due più semplici componenti circuitali: due bipoli. Questo circuito prende il nome di Circuito Elementare.

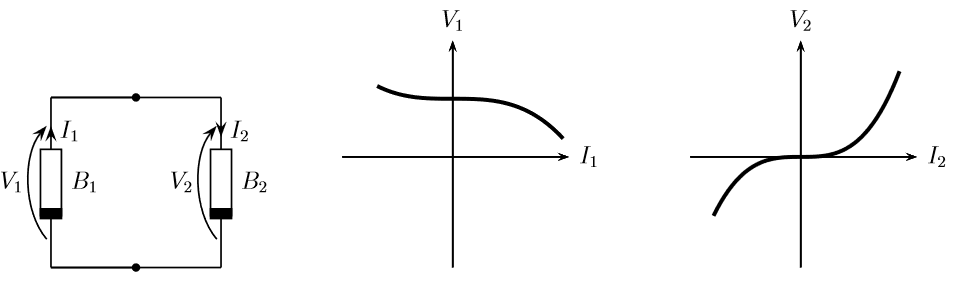
Consideriamo quindi il circuito elementare riportato in figura, composto da due bipoli resistivi B1 e B2 di relazioni costitutive note f1(V1,I1) e f2(V2,I2). Il circuito è composto da due lati e pertanto presenta 4 incognite (tensione e corrente in ogni lato). Per risolverlo occorrerà disporre di 4 equazioni linearmente indipendenti. Queste sono le due relazioni topologiche dettate dalla LKV e dalla LKC e due relazioni costitutive corrispondenti alle due caratteristiche f1 ed f2:

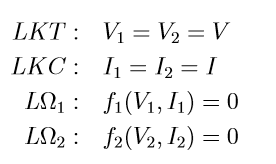
Ci proponiamo di risolvere questo insieme di 4 equazioni mediante un approccio grafico basato sull’uso delle caratteristiche.

Osserviamo innanzitutto che le prime due equazioni, in virtù delle particolari convenzioni di segno scelte (convenzione degli utilizzatori per un bipolo e convenzione degli utilizzatori per l’altro bipolo) ci consentono di definire una unica tensione V ed una unica corrente I comune a quella di entrambe i bipoli; questo fatto ci consente di rappresentare le due caratteristiche f1(V1,I1) = f1(V,I) e f2(V2,I2) = f2(V,I) sullo stesso sistema di assi cartesiani.

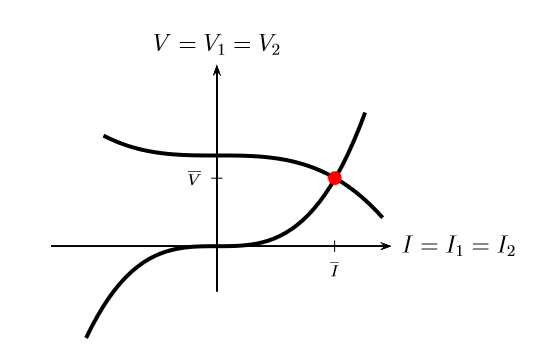
Si può quindi concludere che la coppia (V ,I) rappresenta la soluzione del circuito cercata.

Attenzione: La sovrapposizione delle caratteristiche può esser fatta soltanto se le convenzioni di segno sono tali da poter scrivere le LK nella forma (1) e (2); alternativamente, bisognerà modificare le convenzioni di segno con cui sono rappresentate le caratteristiche dei bipoli in modo da scrivere le LK nella forma V1 = V2 = V e I1 = I2 = I.

Bipoli equivalenti

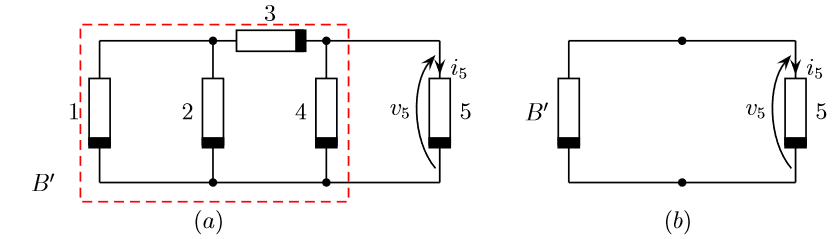
Due bipoli si dicono equivalenti se hanno la stessa caratteristica; ne segue che in un circuito un bipolo B può essere sostituito da un altro bipolo B′ ad esso equivalente senza che il resto del circuito ne venga influenzato in alcun modo. Sfruttando il concetto di equivalenza è quindi possibile passare dal circuito (a) a quello (b) di figura senza che le variabili v5 e i5 ne risentano in alcun modo.

Connessione in serie di due bipoli resistivi

Due bipoli resistivi B1 e B2 connessi come in figura si dicono connessi in serie. L’insieme dei due bipoli connessi in serie forma un nuovo bipolo Bs.

Con le convenzioni di segno riporte in figura la tensione Vs e la corrente Is del bipolo Bs sono legate alle tensioni e correnti di B1 e B2 dalle seguenti due LK:

Vs = V1 + V2 Is = I1 = I2

Inoltre le caratteristiche dei bipoli B1 e B2, essendo resistivi, sono rispettivamente f1(V1,I1) = 0 e f2(V2,i2) = 0. Anche il bipolo equivalente Bs è resistivo ed avrà una caratteristica fs(Vs,Is) = 0 che si può determinare nel seguente modo: per ogni valore di Is la tensione Vs, se esiste, è data dalla somma della tensione V1 di B1, corrispondente al valore di corrente I1 = Is e V2 di B2, corrispondente al valore di corrente I2 = Is.

Si noti che può accadere che nessuna corrente di B1 sia anche corrente di B2; in questo caso la connessione serie di B1 e B2 risulta impossibile.

Connessione in parallelo di due bipoli resistivi

Due bipoli resistivi B1 e B2 connessi come in figura si dicono connessi in parallelo. L’insieme dei due bipoli connessi in parallelo forma un nuovo bipolo Bp.

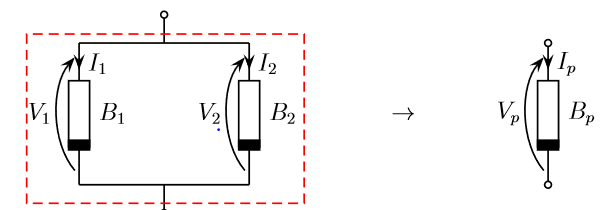
Con le convenzioni di segno riporte in figura la tensione Vp e la corrente Ip del bipolo Bp sono legate alle tensioni e correnti di B1 e B2 dalle seguenti due LK:
Ip = I1 + I2 Vp = V1 = V2

Inoltre le caratteristiche dei bipoli B1 e B2, essendo resistivi, sono rispettivamente f1(V1,I1) = 0 e f2(V2,i2) = 0. Anche il bipolo equivalente Bp è resistivo ed avrà una caratteristica fp(Vp,Ip) = 0 che si può determinare nel seguente modo: per ogni valore di Vp la corrente Ip, se esiste, è data dalla somma della corrente I1 di B1, corrispondente al valore di tensione V1 = Vp e I2 di B2, corrispondente al valore di tensione V2 = Vp.

Si noti che può accadere che nessuna tensione di B1 sia anche tensione di B2; in questo caso la connessione parallelo di B1 e B2 risulta impossibile.

Questi erano bipoli in serie e parallelo 😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!