L’ARTE DI CONTARE

Sei sicuro di saper fare le somme nel modo corretto? Vediamo alcuni esempi concreti in cui il modo “normale” di fare le somme può non essere quello migliore.

Ecco a voi il primo esempio:

Sei in aula (ahimè, forse in questo periodo meglio dire che sei davanti al computer di casa) che fai rumore, e la professoressa ti sente. Per far sì che il resto della classe non sia disturbata, ti mette in punizione dicendoti: “Fai la somma di tutti i numeri compresi tra 1 e 100, e poi dimmi il risultato”.

Tu, che ormai le somme le sai fare benissimo, ti metti all’opera. La somma che dobbiamo fare è bella lunga, sì, però non ci perdiamo d’animo.

1+2+3+4+5+6+7+8+9+10+11+12+….+100… Ogni somma è facile da fare, però è chiaro che ci vorrà un po’ di tempo. Se potessimo utilizzare la calcolatrice forse sarebbe più facile, ma non sarebbe comunque velocissimo. Richiede del tempo digitare tutti i numeri dall’1 al 100. “La prof. mi vuole tenere in punizione per tutto il giorno” potresti pensare. Forse il fatto che ti ci vorrà una vita per fare un calcolo così semplice potrebbe farti pensare di cercare qualche scappatoia. La stessa punizione fu posta al famoso matematico Gauss, quando era ancora alla scuola primaria: pigro com’era, non poteva di certo sprecare così tanto tempo per fare questo calcolo. Spesso dalla pigrizia nasce l’invenzione. Come disse Agata Christie,

“L’invenzione deriva sempre da un certo ozio, forse addirittura da una certa pigrizia”.

Seguendo le orme di Gauss, ti insegno un metodo alternativo per fare questa somma, in modo che ti ci vorranno solo pochi minuti.

Prima di tutto, scrivi tutti i numeri da 1 a 100 in riga, intervallati da un “+”. Nella riga sotto, scriviamo questa stessa somma ma al contrario, in modo che i numeri vadano dal più alto al più basso. Quello che otteniamo è la scrittura seguente:

\(1+2+3+4+\dots+98+99+100\)

\(100+99+98+97+\dots+3+2+1\)

Adesso sommiamo tutti i numeri che ho scritto: “Qual è il vantaggio?” potresti dirmi. “Sto semplicemente eseguendo quella somma due volte. È ancora più lungo!”

Beh, questo dipende da come eseguite questa somma. È come se avessimo una tabella 100×2, con 2 righe e 100 colonne, e dovessimo sommarne tutte le entrate. Se lo facessimo per riga sarebbe molto lungo, ma se sommassimo le entrate per colonna ci accorgeremmo di una cosa molto comoda: il valore della somma su ogni colonna è 101! Se non ti è chiaro, guarda questa tabella.

Quindi per sommare tutte le entrate non ci resta che sommare tra loro i 101: quanti sono? Beh, sono 100, perché ce ne è uno per ogni colonna. Perciò la somma finale di tutte le entrate della tabella sarà data da

\(100\cdot 101\).

Questo è il risultato che mi ha chiesto la professoressa? No, perché ho effettuato due volte la somma richiesta: ricordiamoci che abbiamo dovuto riscrivere la stessa somma in ordine decrescente per utilizzare questo trucco. Quindi la somma della sola prima riga sarà esattamente la metà del risultato ottenuto. Perciò

\(1+2+3+\dots+98+99+100=\frac{100\cdot 101}{2}=5050\).

La cosa geniale di questo metodo non è tanto il fatto che riduce notevolmente i tempi di calcolo (cosa comunque importantissima), ma il fatto che può essere generalizzata a qualsiasi numero. Se la professoressa, non contenta del fatto che ci hai messo troppo poco e la tua punizione è già finita, ti dicesse di calcolare la somma di tutti i numeri compresi tra 1 e 1.000, il metodo richiederebbe esattamente lo stesso tempo! Infatti il risultato sarebbe \(\frac{1.000 \cdot 1.001}{2}=500.500\). Se vuoi, puoi controllare che per ogni numero naturale \(n\) la somma dei numeri compresi tra 1 e n è data da questa formula

\(\sum_{k=1}^n k = \frac{n\cdot (n+1)}{2}\) .

Il simbolo a sinistra è una sommatoria, e ha il significato di sommare tutti i termini presenti dopo di essa facendo variare \(k\) tra \(1\) e \(n\) (nel nostro caso è equivalente a scrivere \(1+2+3+\dots+(n-2)+(n-1)+n\)).

Passiamo al secondo esempio.

La situazione è la stessa di prima, però la richiesta è diversa. La punizione consiste nel fare la somma dei primi 100 numeri dispari.

Per intenderci, la somma che devi fare è \(1+3+5+7+\dots+199\). Come prima, i conti a mano sono troppo lunghi, e la calcolatrice non si può usare (ma anche se si potesse usare sicuramente non sarebbe un lavoro velocissimo). Riadattando il metodo di Gauss visto in precedenza a questa situazione, puoi ottenere un risultato soddisfacente in poco tempo. Tuttavia voglio mostrarti un altro metodo più geometrico, applicabile a questa particolare situazione.

I numeri possono essere pensati intuitivamente come un insieme di oggetti, per semplicità dei pallini. Fin dalla loro introduzione, infatti, la loro principale utilità era quella di determinare il numero degli oggetti di un insieme, in modo che si potesse dare una risposta soddisfacente a domande del tipo “Quanti sono questi buoi?”. Dunque, il numero 1 è un singolo pallino, il numero 3 è un insieme di tre pallini, e così via. Contare quanto vale la somma dei primi 100 numeri dispari significa allora raggruppare tutti i pallini che descrivono questi 100 numeri e contare quanti sono.

Risulta fondamentale disporre questi pallini in un modo che ci faciliti la vita. Facciamolo dunque in questo modo: mettiamo in basso a sinistra il primo pallino che descrive il numero 1. Successivamente mettiamo i tre pallini che descrivono il 3 come in figura.

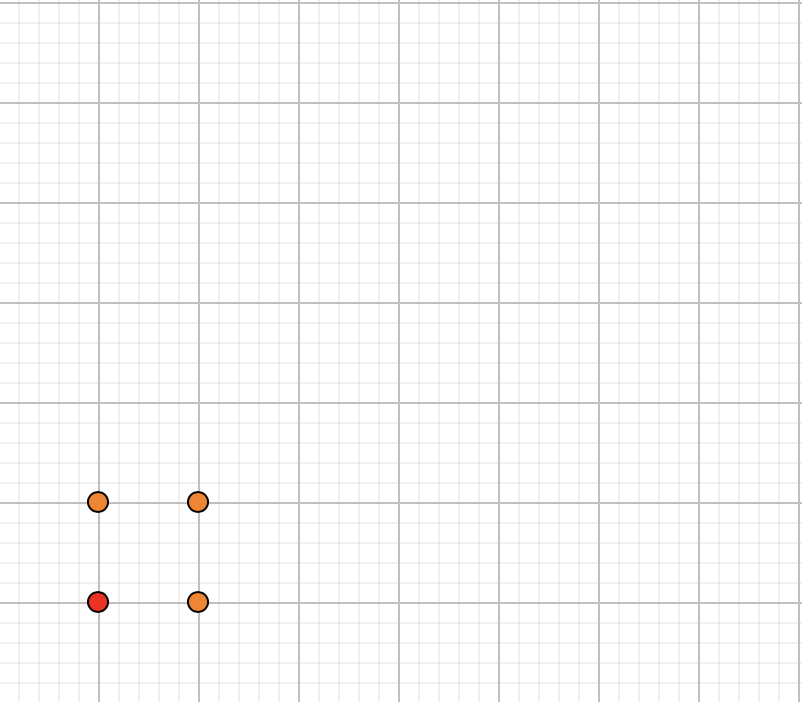
Osserviamo che i pallini descrivono un quadrato 2×2. Aggiungere il terzo numero dispari (cioè 5), significa aggiungere altri cinque pallini, ed è possibile farlo mantenendo la struttura quadrata, come vediamo in figura.

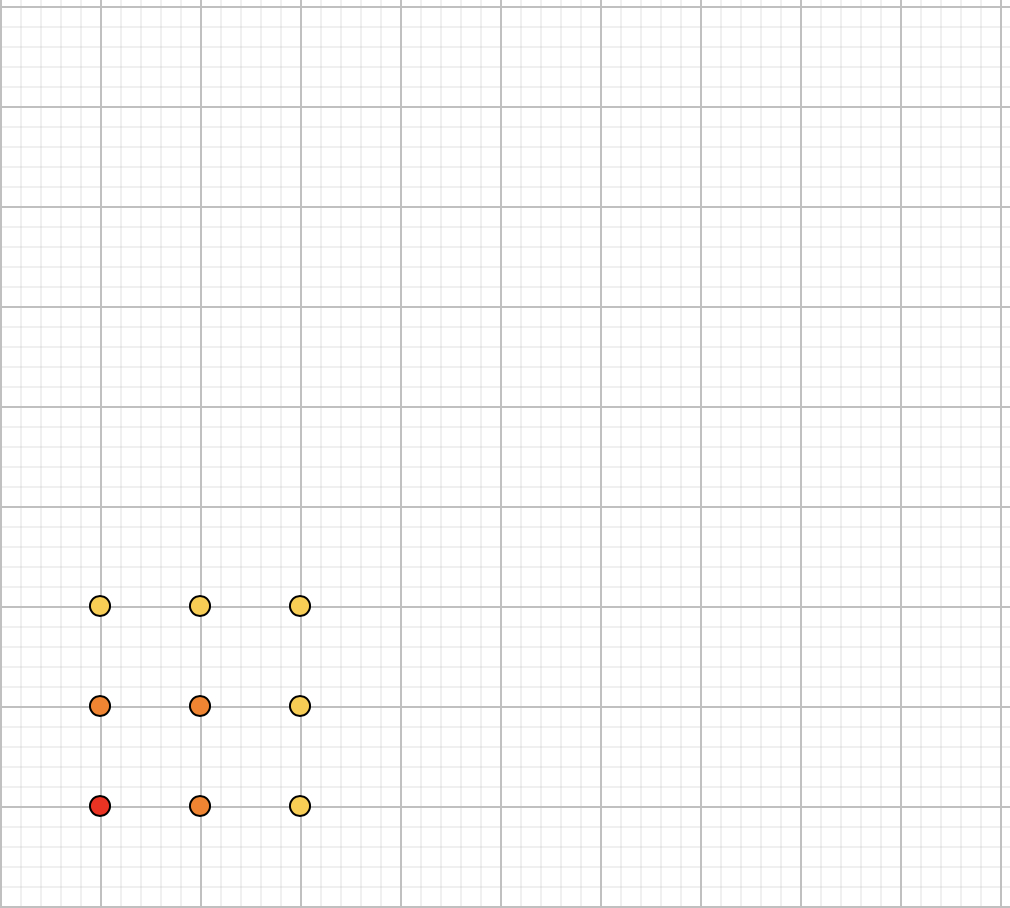
È chiaro allora che, quando sommo i primi due numeri dispari i pallini formano un quadrato di lato 2 (nel senso che su ogni lato ci sono due pallini), quando sommo i primi tre numeri dispari i pallini formano un quadrato di lato 3 e così via. Sommando i primi 100 numeri dispari, come ci è chiesto dalla professoressa, otteniamo un quadrato di lato 100, come esemplificato in figura.

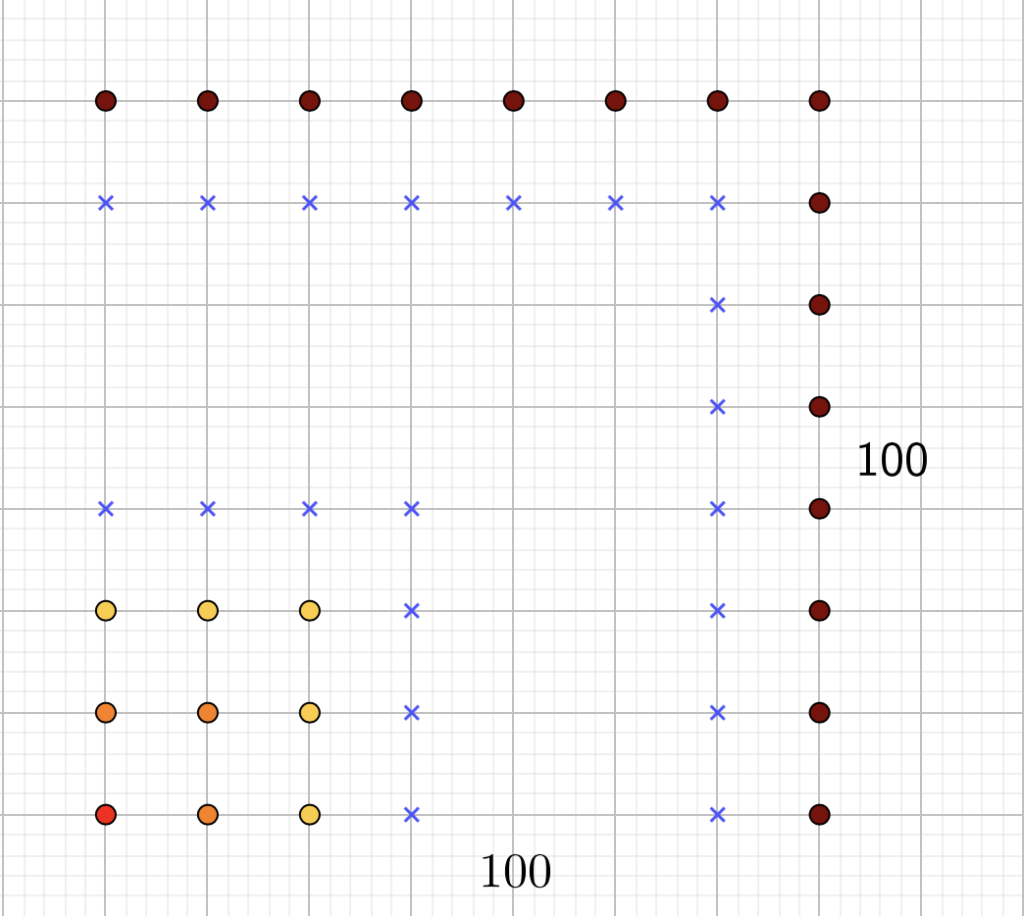
Perciò contare il numero di questi pallini è facile: basta capire quanti pallini ci sono in un quadrato 100×100, cioè \(100^2\)!

Abbiamo ottenuto la seguente formula:

\(1+3+5+\dots+197+199=100^2=10.000\).

Anche in questo caso il ragionamento può essere generalizzato! La somma dei primi \(n\) numeri dispari è semplicemente il numero di pallini presenti in un quadrato in cui su ogni lato sono presenti \(n\) pallini, cioè \(n^2\)! Dunque

\(\sum_{k=1}^{n} (2k-1) = n^2\),

dove ancora una volta la sommatoria è un modo più elegante per scrivere la somma dei primi \(n\) numeri dispari.

Questi erano alcuni consigli per coltivare “l’arte di contare”! 😉
Speriamo che tu possa aver trovato utile questo nostro articolo. Se hai domande o commenti non esitare a scrivere qui sotto.