Teorema Fondamentale del Calcolo Integrale

Dopo aver introdotto, nello scorso articolo, il concetto di integrale definito, oggi scopriremo uno strumento potentissimo per calcolare le aree sottese da grafici di funzioni: il teorema fondamentale del calcolo integrale!

Introduciamo inizialmente il concetto di funzione integrale.

Sia data \(f:[a,b]\to\mathbb{R}\), funzione limitata e R-integrabile su \([a,b]\). Si chiama funzione integrale di \(f\) in \([a,b]\) la funzione
\(F(x) := \int_a^x f(t)dt\).

Per come è definita, \(F\) è una funzione che riceve in ingresso un numero \(x\in[a,b]\) e restituisce un nuovo numero, che rappresenta l’area con segno sottesa dal grafico della funzione \(f\) tra \(a\) e \(x\), come si nota in figura.

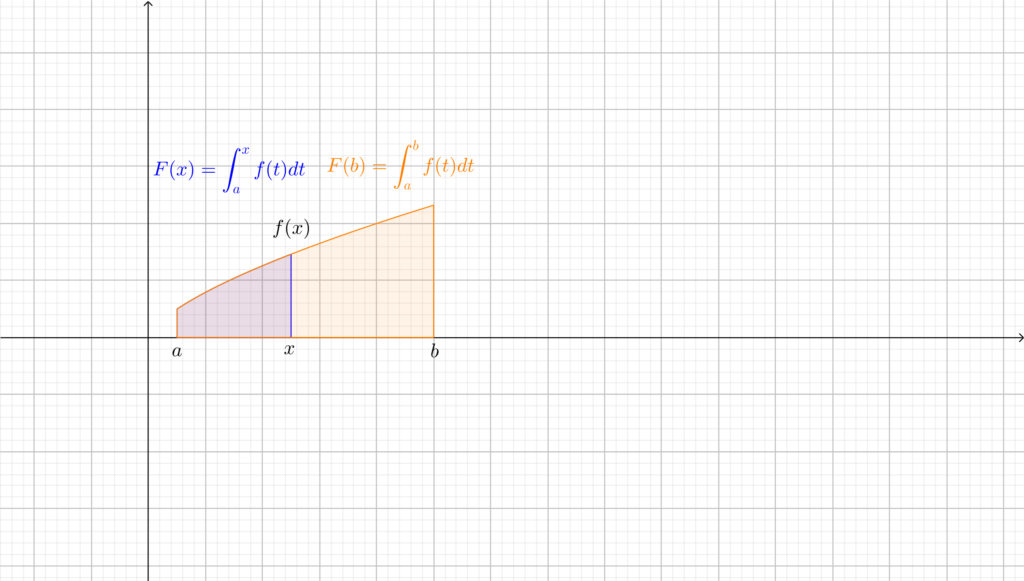
Osserviamo che \(F(a)=\int_a^a f(t)dt=0\), perchè si tratta di un’area nulla. Inoltre \(F(b)=\int_a^b f(t)dt\), l’area sottesa dal grafico di \(f\) in tutto l’intevallo \([a,b]\). L’obiettivo è trovare un modo intelligente per calcolare quest’area.

Essendo \(F\) una funzione, ha senso chiedersi se questa sia continua e derivabile in \([a,b]\); in particolare, quello che vorremmo fare è stabilire una relazione tra la funzione integranda \(f\) e la funzione integrale \(F\). Ci si accorge che c’è una stretta relazione tra la derivata della funzione integrale e la funzione integranda. Infatti \(F'(x)\) rappresenta, in base al significato di derivata, la rapidità con cui aumenta \(F\), cioè la rapidità con cui aumenta l’area (con segno) sottesa dal grafico di \(f\) tra \(a\) e \(x\), al variare di \(x\).

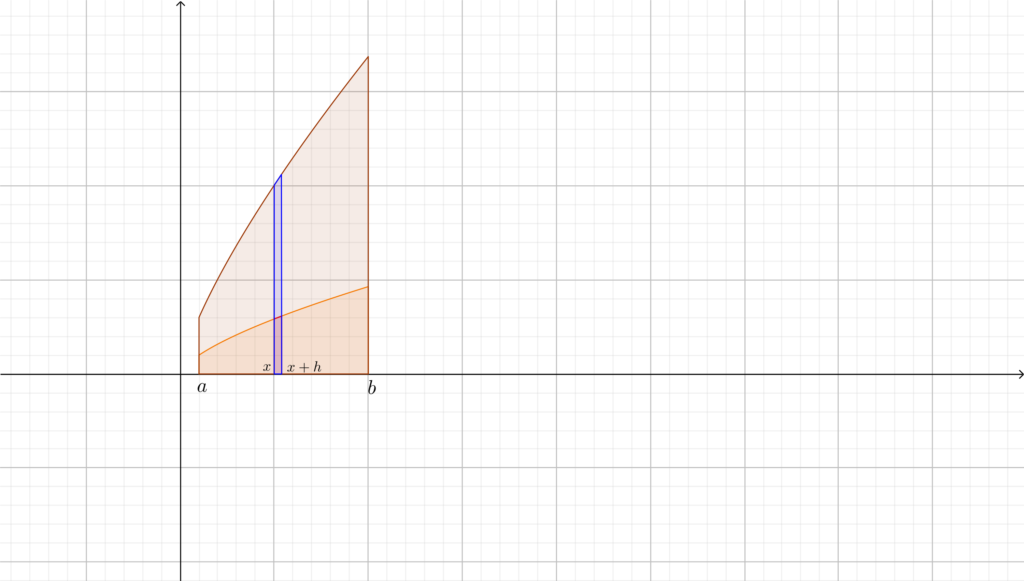
Ad esempio, dal grafico di queste due funzioni risulta chiaro che la rapidità con cui cresce l’area tra \(a\) e \(x\) è strettamente collegata al valore di \(f\) in \(x\). Andiamo dunque a formalizzare questi concetti con il seguente teorema, che, come suggerisce il nome, è molto importante.

Dimostrazione.

(a) Sia \(x_0\in[a,b]\). Voglio mostrare che \(F\) è continua in \(x_0\), cioè che \(\lim_{x\to x_0}F(x)=F(x_0)(=\int_a^{x_0} f(t)dt) .\)
Ricordando la definizione di funzione integrale, andiamo a calcolare tale limite.

\(\lim_{x\to x_0}F(x)=\lim_{x\to x_0} \int_a^x f(t)dt=\)

\(=\lim_{x\to x_0} (\int_a^{x_0}f(t)dt+\int_{x_0}^x f(t)dt)=\)

\(=\int_a^{x_0}f(t)dt+\lim_{x\to x_0}\int_{x_0}^x f(t)dt\),

dove l’ultima uguaglianza vale perchè il primo termine della somma non dipende da \(x\). Abbiamo quindi scoperto che

\(\lim_{x\to x_0}F(x)=F(x_0)+ \lim_{x\to x_0} \int_{x_0}^x f(t)dt\).

L’unica cosa che rimane da mostrare per concludere il punto (a) è che

\(\lim_{x\to x_0} \int_{x_0}^x f(t)dt=0. \)
Facciamolo utilizzando il teorema del confronto, noto anche come teorema dei due carabinieri, mostrando che la quantità di cui fare il limite è compresa tra due quantità tendenti a zero.

Infattti il fatto che \(f\) sia R-integrabile su \([a,b]\) garantisce che sia limitatà, cioè che \(\exists M\in\mathbb{R}^+ \colon -M<f(x)<M\) \(\forall x\in [a,b]\). Quindi segue che

\(\int_{x_0}^x -M dx < \int_{x_0}^x f(t)dt < \int_{x_0}^x M dx \quad \Rightarrow \quad -M(x-x_0)<\int_{x_0}^x f(t)dt < M(x-x_0)\), essendo la prima e l’ultima delle aree (con segno) di rettangoli di base \(x-x_0\) e altezza \(\pm M\). Dunque

\(0=\lim_{x\to x_0} -M(x-x_0)< \lim_{x\to x_0} \int_{x_0}^x f(t)dt < \lim_{x\to x_0} M(x-x_0)=0.\) Perciò per il teorema dei due carabinieri \(\lim_{x\to x_0}\int_{x_0}^x f(t)dt =0\), come volevasi dimostrare. La continuità di \(F\) è dunque dimostrata.

(b) Sia \(x_0\in (a,b)\) e supponiamo \(f\) continua in \(x_0\). Vogliamo mostrare non solo che \(F\) è derivabile in \(x_0\), cioè che esiste finito il rapporto incrementale, ma anche che \(F'(x_0)=f(x_0)\).

Dunque dobbiamo dimostrare che \(\lim_{h\to 0} \frac{F(x_0+h)-F(x_0)}{h}=f(x_0). \)

Andiamo dunque a esplicitare il rapporto incrementale centrato in \(x_0\), chiamandolo \(R.I.(x_0)\):

\(R.I.(x_0)= \frac{F(x_0+h)-F(x_0)}{h}\)

\(=\frac{\int_a^{x_0+h}f(t)dt – \int_a^{x_0}f(t)dt}{h}=\)

\(=\frac{\int_{x_0}^{x_0+h}f(t)dt}{h}.\)

Chiaramente \(\lim_{h\to 0} R.I(x_0)=f(x_0) \iff \lim_{h\to 0} R.I.(x_0)-f(x_0)=0.\)

Ora, poichè \(\int_{x_0}^{x_0+h}f(x_0)dt=base\cdot altezza= f(x_0)\cdot h\), allora \(R.I.(x_0)-f(x_0)=\frac{\int_{x_0}^{x_0+h}f(t)dt}{h}-\frac{\int_{x_0}^{x_0+h}f(x_0)dt}{h}=\frac{\int_{x_0}^{x_0+h}(f(t)-f(x_0))dt}{h}.\) A questo punto si può sfruttare la continuità della funzione \(f\) in \(x_0\).

Fissato \(\epsilon >0\) esiste \(\delta >0\) per cui, se \(t\) è tale che \(|t-x_0|<\delta\), allora \(|f(t)-f(x_0)|<\epsilon\).

Consideriamo quindi \(h\) sufficientemente piccolo (possiamo farlo perchè sta tendendo a zero) tale per cui \(0<|h|<\delta\). Necessariamente se \(t\in[x_0,x_0+h]\), allora \(|t-x_0|<\delta\) e per la continuità di \(f\) avremo \(|f(t)-f(x_0)|<\epsilon\).

Dunque $latex|R.I.(x_0)-f(x_0)|= \frac{1}{|h|}|\int_{x_0}^{x_0+h} (f(t)-f(x_0))dt|\le$

\(\le \frac{1}{|h|}\int_{x_0}^{x_0+h}|f(t)-f(x_0)|dt <\)

\(< \frac {1}{|h|}\int_{x_0}^{x_0+h}|\epsilon|dt=\epsilon.\)

Abbiamo dimostrato che per ogni \(\epsilon>0\) esiste \(\delta >0\) tale che, se \(0<|h|<\delta\), allora \(|R.I.(x_0)-f(x_0)|<\epsilon\), cioè \(\lim_{h\to 0} \frac{F(x_0+h)-F(x_0)}{h}=f(x_0)\), che è la tesi.

Fine della dimostrazione

Una conseguenza immediata di questo teorema è che se \(f:[a,b]\to\mathbb{R}\) è continua \(\forall x\in[a,b]\), allora \(F(x)\), la sua funzione integrale, è derivabile in ogni \(x\in (a,b)\) e \(F'(x)=f(x)\) \(\forall x\in (a,b)\). Perciò ogni funzione continua su un intervallo \([a,b]\) ammette almeno una primitiva: la sua funzione integrale!

A questo punto siamo pronti per dimostrare una formula molto utile per calcolare aree con segno sottese da grafici di funzioni. Infatti farlo utilizzando la definizione e l’approssimazione in rettangoli è molto scomodo. Fortunatamente viene in soccorso la seguente formula.

Prima di dimostrare questa formula, è utile osservare che data una funzione \(f\) che ammette primitiva su un intervallo \(I\), la famiglia delle sue primitive su \(I\) una famiglia di funzioni che differiscono per una costante, cioè

(*): “Se \(\varphi_1\) e \(\varphi_2\) sono entrambe primitive di \(f\) sull’intervallo \(I\subseteq \mathbb{R}\), allora

\( \varphi_1(x)=\varphi_2(x)+c\) per qualche \(c\in\mathbb{R}\).”

Esercizio (Bonus). Dimostrare l’affermazione (*). L’affermazione vale anche se \(I\) non è un intervallo? Ad esempio \(I=(-\infty,0)\cup(0,+\infty)\). Giustificare la risposta.

Dimostrazione della formula.

Sia \(\varphi\) una primitiva di \(f\) su \((a,b)\). Come dimostrato in precedenza, anche \(F(x)=\int_a^x f(t)dt\) è una primitiva di \(f\) su tale intervallo. Quindi in base all’affermazione (*) \(F\) e \(\varphi\) differiscono per una costante \(C\in\mathbb{R}\). Quindi \(F(x)=\varphi(x)+C\)

\( \Rightarrow \int_a^x f(t)dt=\varphi(x)+C.\)
Per determinare la costante \(C\), valutiamo l’espressione in \(a\). Dunque \(\int_a^a f(t)dt=\varphi(a)+C\)

\(\Rightarrow \quad 0=\varphi(a)+C \)

\( \Rightarrow \quad C=-\varphi(a).\)
Pertanto inserendo il valore di \(C\)

\(\int_a^x f(t)dt=\varphi(x)-\varphi(a)\), \(\forall x\in[a,b] \).
Per concludere la dimostrazione non resta che valutare questa espressione in \(b\), ottenendo \(\int_a^b f(t)dt=\varphi(b)-\varphi(a).\)
Fine della dimostrazione.

Abbiamo dunque scoperto una formula che può risultare molto utile negli esercizi per calcolare il valore di aree e di integrali definiti.

Questo era il Teorema Fondamentale del Calcolo Integrale  😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!